Реакция на заявление
Заявление NIST вызвало поток критических замечаний и обвинений. К сожалению, они были скорее политическими, чем научными. RSA Data Security, Inc., продающая алгоритм RSA, возглавила критиков DSS. Они требовали, чтобы в стандарт использовался алгоритм RSA. RSADSI получило немало денег за лицензирование алгоритма RSA, и стандарт бесплатной цифровой подписи прямо повлиял бы на самую суть ее коммерческих успехов. (Примечание: DSA необязательно не нарушает патенты, мы рассмотрим эту тему позднее.)
До заявления о принятии алгоритма RSADSI вело компанию против "общего модуля,'' который, возможно, позволит правительству подделывать подписи. Когда было объявлено, что алгоритм не использует общий модуль, критика была продолжена с других позиций [154], как с помощью писем в NIST, так и с помощью заявлений в прессе. (Четыре письма в NIST появилось в [1326]. Читая их, не забывайте, что по крайней мере два автора, Ривест и Хеллман, были финансово заинтересованы в том, чтобы DSS не был принят.)
Многие большие компании, разрабатывающие программное обеспечение, которые уже лицензировали алгоритм RSA, также выступили против DSS. В 1982 году правительство попросило предоставить ему алгоритмы с открытым ключом для выбора одного из них в качестве стандарта [537]. После этого в течение девяти лет от NIST не было никаких известий. Такие компании, как IBM, Apple, Novell, Lotus, Northern Telecom, Microsoft, DEC и Sun потратили много денег, реализуя алгоритм RSA. Они не были заинтересованы в потере инвестиций.
Всего к концу первого периода обсуждения(28 февраля 1992 года) NIST получил 109 замечаний. Рассмотрим по порядку критические замечания в адрес DSA.
1. DSA нельзя использовать для шифрования или распределения ключей.
Правильно, но стандарт и не требует наличия этих возможностей. Это стандарт подписи. NIST подготовить стандарт шифрования с открытым ключом. NIST совершает большую ошибку, оставляя американский народ без стандарта шифрования с открытым ключом. По всей вероятности предложенный стандарт цифровой подписи будет невозможно использовать для шифрования. (Но оказывается, что возможно - см. раздел 23.3.) Это не означает, что стандарт подписи бесполезен.
2. DSA был разработан NSA, и в алгоритме могут быть специальные лазейки.
Большинство первоначальных комментариев были просто параноидальными: "Отрицание NIST существующих алгоритмов без видимых причин не внушает доверия к DSS, а усиливает подозрение, что существует тайная программа, стремящаяся позволить NIST и/или NSA вскрывать национальную криптосистему с открытым ключом" [154]. Серьезный вопрос относительно безопасности DSA был задан Аржаном Ленстрой (Arjen Lenstra) и Стюартом Хабером (Stuart Haber) из Bellcore. Он будет рассмотрен ниже.
3. DSA медленнее RSA [800].
Более или менее справедливо. Скорости генерации подписи примерно одинаковы, но проверка подписи с помощью DSA от 10 до 40 раз медленнее. Однако генерация ключей быстрее. Но эта операция неинтересна, пользователь редко применяет ее. С другой стороны проверка подписи - это наиболее частая операция.
Проблема критики в том, что существует много способов поиграть параметрами тестирования, добиваясь нужных результатов. Предварительные вычисления могут ускорить генерацию подписи DSA, но они не всегда возможны. Сторонники RSA подбираят числа так, чтобы выделить преимущества своего алгоритма, а сторонники DSA используют свой способ оптимизации. В любом случае компьютеры становятся все быстрее и быстрее. Хотя разница в скорости и существует, в большинстве приложений она не будет заметна.
4. RSA - это стандарт de facto.
Вот два примера подобных жалоб. Письмо Роберта Фоллета (Robert Follett), директора программы стандартизации компании IBM [570]:
IBM считает, что NIST предложил стандарт схемы цифровой подписи, отличающийся от принимаемых международных стандартов. Пользователи и организации пользователей убедили нас в том, что поддержка международных стандартов, использующих RSA, в самом ближайшем будущем станет необходимым условием продажи средств обеспечения безопасности.
Письмо Леса Шроера (Les Shroyer), вице-презитента и директора компании Motorola [1444]:
У нас должен быть единый, надежный, признанный всеми алгоритм цифровой подписи, который можно использовать по всему миру как между американскими и неамериканскими объектами, òàê è ìåæäó системами êîìïàíèè Motorola и системами других производителей. Отсутствие других жизнеспособных технологий цифровой подписи за последние восемь лет сделало RSA фактическим стандартом. . . . Motorola и многие другие компании. . . вложили в RSA миллионы долларов. Мы сомневаемся во взаимодействии и возможности поддержки двух различных стандартов, такое положение приведет к росту расходов, задержек развертывания и усложнению систем. . . .
Многим компаниям хотелось, чтобы NIST принял ISO 9796, международный стандарт цифровой подписи, использующий RSA [762.]. Хотя это и серьезный аргумент, он недостаточен, чтобы принять международный стандарт в качестве национального. Бесплатный стандарт лучше отвечал бы общественным интересам Соединенных Штатов.
5. Выбор национального алгоритма не был открытым, не было дано достаточно времени для анализа.
Сначала NIST утверждал, что разработал DSA самостоятельно, затем признал помощь NSA. Наконец NIST подтвердил, что NSA является автором алгоритма. Это многих обеспокоило - NSA не внушает людям доверие. Даже так, алгоритм был опубликован и доступен для анализа, кроме того, NIST продлил время анализа и комментирования алгоритма.
6. DSA может нарушать другие патенты. Это так. Этот вопрос будет рассмотрен в разделе, рассматривающим патенты.
7. Размер ключа слишком мал.
Это единственно справедливая критика DSS. Первоначально предлагалось использовать модуль длиной 512 битов [1149]. Так как безопасность алгоритма определяется сложностью вычисления дискретных логарифмов по заданному модулю, этот вопрос волновал многих криптографов. С тех пор вычисление дискретных логарифмов в конечном поле достигло определенных успехов, и 512 битов слишком мало для долговременной подписи (см. раздел 7.2). Согласно Браяну ЛаМаччиа (Brian LaMacchia) и Эндрю Одлыжко (Andrew Odlyzko), " . . . даже безопасность, обеспечиваемая 512-битовыми простыми числами, по видимому, находится на пределе . . . " [934]. В ответ на эти замечания NIST сделал длину ключа переменной, от 512 до 1024 битов. Немного, но все-таки получше.
19 мая 1994 года был издан окончательный вариант стандарта [1154]. При этом было сказано [542]:
Этот стандарт может применяться всеми Федеральными департаментами и управлениями для защиты несекретной информации. . . . Этот стандарт будет использован при проектировании и реализации схем подписи с открытыми ключами, которые разрабатывают Федеральные департаменты и управления, или которые разрабатываются по из заказу. Частные и коммерческие организации могут принять и использовать этот стандарт.
Прежде чем пользоваться этим стандартом и реализовывать его, прочтите ниже раздел о патентах.
Описание DSA
DSA, представляющий собой вариант алгоритмов подписи Schnorr и EIGamal, полностью описан в [1154]. Алгоритм использует следующие параметры:
p = простое число длиной Lбитов, где L принимает значение, кратное 64, в диапазоне от 512 до 1024. (В первоначальном стандарте размер pбыл фиксирован и равен 512 битам [1149]. Это вызвало множество критических замечаний, и NIST этот пункт алгоритма [1154].)
q= 160-битовой простое число - множитель p-1.
g= h(p-1)/qmod p, где h- любое число, меньшее p-1, для которого h(p-1)/qmod p больше 1.
x = число, меньшее q.
y= gxmod p.
В алгоритме также используется однонаправленная хэш-функция: H(m). Стандарт определяет использование SHA, рассмотренного в разделе 18.7.
Первые три параметра, p, q и g, открыты и могут быть общими для пользователей сети. Закрытым ключом является x, а открытым - y. Чтобы подписать сообщение, m:
(1) Àëèñà генерирует случайное число k, меньшее q
(2) Àëèñà генерирует
r= (gk mod p)mod q
s = (k-1(H(m)+ xr))mod q
Ее подписью служат параметры rи s, она посылает их Áîáу.
(3) Áîá проверяет подпись, вычисляя
w = s-1 mod q
u1 = (H(m) * w)mod q
u2 = (rw)mod q
v= (( 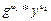 ) mod p) mod q
) mod p) mod q
Если v= r, то подпись правильна.
Доказательства математических соотношений можно найти в [1154]. Табл. 20-1 представляет собой краткое описание алгоритма.
Табл. 20-1.
Подписи DSA
Открытый ключ:
| p | простое число длиной от 512 до 1024 битов (может использоваться группой пользователей) |
| q | 160-битовый простой множитель p-1 (может использоваться группой пользователей) |
| g | = h(p-1)/qmod p, где h- любое число, меньшее p-1, для которого h(p-1)/qmod p > 1 (может использоваться группой пользователей) |
| y | = gxmod p (p-битовое число) |
Закрытый ключ:
| x | < q (160-битовое число) |
Подпись:
| k | выбирается случайно, меньшее q |
| r | (подпись) = (gk mod p)mod q |
| s | (подпись) = (k-1(H(m)+ xr))mod q |
Проверка:
| w | = s-1 mod q |
| u1 | = (H(m) * w)mod q |
| u2 | = (rw)mod q |
| v | = (( 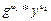 ) mod p) mod q ) mod p) mod q
|
| Если v= r, то подпись правильна. |
Дата добавления: 2021-01-26; просмотров: 551;











