Сложность алгоритмов
Сложность алгоритма определяется вычислительными мощностями, необходимыми для его выполнения. Вычислительная сложность алгоритма часто измеряется двумя параметрами: T (временная сложность) и S (пространственная сложность, или требования к памяти). И T, и S обычно представляются в виде функций от n, где n - это размер входных данных. (Существую и другие способы измерения сложности: количество случайных бит, ширина канала связи, объем данных и т.п.)
Обычно вычислительная сложность алгоритма выражается с помощью нотации "О большого", т.е описывается порядком величины вычислительной сложности. Это просто член разложения функции сложности, быстрее всего растущий с ростом n, все члены низшего порядка игнорируются. Например, если временная сложность данного алгоритма равна 4n2+7n+12, то вычислительная сложность порядка n2, записываемая как O(n2).
Временная сложность измеренная таким образом не зависит от реализации. Не нужно знать ни точное время выполнения различных инструкций, ни число битов, используемых для представления различных переменных, ни даже скорость процессора. Один компьютер может быть на 50 процентов быстрее другого, а у третьего шина данных может быть в два раза шире, но сложность алгоритма, оцененная по прядку величины, не изменится. Это не жульничество, при работе с алгоритмами настолько сложными, как описанные в этой книге, всем прочим можно пренебречь (с точностью до постоянного множителя) в сравнении со сложностью по порядку величины.
Эта нотация позволяет увидеть, как объем входных данных влияет на требования к времени и объему памяти. Например, если Ò= O(n), то удвоение входных данных удвоит и время выполнения алгоритма. Если Ò=О(2n), то добавление одного бита к входным данным удвоит время выполнения алгоритма.
Обычно алгоритмы классифицируются в соответствии с их временной или пространственной сложностью. Алгоритм называют постоянным, если его сложность не зависит от n: O(1). Алгоритм является линейным, если его временная сложность O(n). Алгоритмы могут быть квадратичными, кубическими и т.д. Все эти алгоритмы - полиномиальны, их сложность - O(nm), где m - константа. Алгоритмы с полиномиальной временной сложностью называются алгоритмами с полиномиальным временем.
Алгоритмы, сложность которых равна О(tf(n)), где t - константа, большая, чем 1, а f(n) - некоторая полиномиальная функция от n, называются экспоненциальными. Подмножество экспоненциальных алгоритмов, сложность которых равна О(cf(n)), где где c - константа, а f(n) возрастает быстрее, чем постоянная, но медленнее, чем линейная функция, называется суперполиномиальным.
В идеале, криптограф хотел бы утверждать, что алгоритм, лучший для взлома спроектированного алгоритма шифрования, обладает экспоненциальной временной сложностью. На практике, самые сильные утверждения, которые могут быть сделаны при текущем состоянии теории вычислительной сложности, имеют форму "все известные алгоритмы вскрытия данной криптосистемы обладают суперполиномиальной временной сложностью". То есть, известные нам алгоритмы вскрытия обладают суперполиномиальной временной сложностью, но пока невозможно доказать, что не может быть открыт алгоритм вскрытия с полиномиальной временной сложностью. Развитие теории вычислительной сложности возможно когда-нибудь позволит создать алгоритмы, для которых существование алгоритмов с полиномиальным временем вскрытия может быть исключено с математической точностью.
С ростом n временная сложность алгоритмов может стать настолько огромной, что это повлияет на практическую реализуемость алгоритма. В Табл. 11-2 показано время выполнения для различных классов алгоритмов при n равном одному миллиону. В таблице игнорируются постоянные величины, но показано, почему это можно делать.
Табл. 11-2
Время выполнения для различных классов алгоритмов
| Класс | Сложность | Количество операций для n=106 | Время при 106 операций в секунду |
| Постоянные | О(1) | 1 мкс | |
| Линейные | О(n) | 106 | 1 с |
| Квадратичные | О(n2) | 1012 | 11.6 дня |
| Кубические | О(n3) | 1018 | 32000 лет |
| Экспоненциальные | О(2n) | 10301030 | В 10301006 раз больше, чем время существования вселенной |
При условии, что единицей времени для нашего компьютера является микросекунда, компьютер может выполнить постоянный алгоритм за микросекунду, линейный - за секунду, а квадратичный - за 11.6 дня. Выполнение кубического алгоритма потребует 32 тысяч лет, что в принципе реализуемо, компьютер, конструкция которого позволила бы ему противостоять следующему ледниковому периоду, в конце концов получил бы решение. Выполнение экспоненциального алгоритма тщетно, независимо от экстраполяции роста мощи компьютеров, параллельной обработки или контактов с инопланетным суперразумом.
Взглянем на проблему вскрытия алгоритма шифрования грубой силой. Временная сложность такого вскрытия пропорциональна количеству возможных ключей, которое экспоненциально зависит от длины ключа. Если n - длина ключа, то сложность вскрытия грубой силой равна О(2n). В разделе 12.3 рассматривается дискуссия об использовании для DES 56-битового ключа вместо 112-битового. Сложность вскрытия грубой силой при 56-битовом ключе составляет 256, а при 112-битовом ключе - 2112. В первом случае вскрытие возможно, а во втором - нет.
Сложность проблем
Теория сложности также классифицирует и сложность самих проблем, а не только сложность конкретных алгоритмов решения проблемы. (Отличным введением в эту тему являются [600, 211, 1226], см. также [1096, 27, 739].) Теория рассматривает минимальное время и объем памяти, необходимые для решения самого трудного варианта проблемы на теоретическом компьютере, известном как машина Тьюринга. Машина Тьюринга представляет собой конечный автомат с бесконечной лентой памяти для чтения-записи и является реалистичной моделью вычислений.
Проблемы, которые можно решить с помощью алгоритмов с полиномиальным временем, называются решаемыми, потому что для разумных входных данных обычно могут быть решены за разумное время. (Точное определение "разумности" зависит от конкретных обстоятельств.) Проблемы, которые невозможно решить за полиномиальное время, называются нерешаемыми, потому что вычисление их решений быстро становится невозможным. Нерешаемые проблемы иногда называют трудными. Проблемы, которые могут быть решены только с помощью суперполиномиальных алгоритмов, вычислительно нерешаемы, даже при относительно малых значениях n.
Что еще хуже, Алан Тьюринг доказал, что некоторые проблемы принципиально неразрешимы. Даже отвлекаясь от временной сложности алгоритма, невозможно создать алгоритм решения этих проблем.
Проблемы можно разбить на классы в соответствии со сложностью их решения. Самые важные классы и их предполагаемые соотношения показаны на Рис. 11-1. (К несчастью, лишь малая часть этих утверждений может быть доказана математически.)
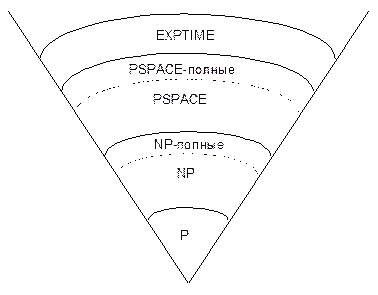
Рис. 11-1. Классы сложности
Находящийся в самом низу класс P состоит из всех проблем, которые можно решить за полиномиальное время. Класс NP - из всех проблем, которые можно решить за полиномиальное время только на недетерминированной машине Тьюринга: вариант обычной машины Тьюринга, которая может делать предположения. Машина предполагает решение проблемы - либо "удачно угадывая", либо перебирая все предположения параллельно - и проверяет свое предположение за полиномиальное время.
Важность NP в криптографии состоит в следующем: многие симметричные алгоритмы и алгоритмы с открытыми ключами могут быть взломаны за недетерминированное полиномиальное время. Для данного шифротекста C, криптоаналитик просто угадывает открытый текст, X, и ключ, k, и за полиномиальное время выполняет алгоритм шифрования со входами X и k и проверяет, равен ли результат C. Это имеет важное теоретическое значение, потому что устанавливает верхнюю границу сложности криптоанализа этих алгоритмов. На практике, конечно же, это выполняемый за полиномиальное время детерминированный алгоритм, который и ищет криптоаналитик. Более того, этот аргумент неприменим ко всем классам шифров, конкретно, он не применим для одноразовых блокнотов - для любого C существует множество пар X, k, дающих C при выполнении алгоритма шифрования, но большинство этих X представляют собой бессмысленные, недопустимые открытые тексты.
Класс NP включает класс P, так как любая проблема, решаемая за полиномиальное время на детерминированной машине Тьюринга, будет также решена за полиномиальное время на недетерминированной машине Тьюринга, просто пропускается этап предположения.
Если все NP проблемы решаются за полиномиальное время на детерминированной машине, то P = NP. Хотя кажется очевидным, что некоторые NP проблемы намного сложнее других (вскрытие алгоритма шифрования грубой силой против шифрования произвольного блока шифротекста), никогда не было доказано, что P ¹ NP (или что P = NP). Однако, большинство людей, работающих над теорией сложности, убеждены, что эти классы неравны.
Что удивительно, можно доказать, что конкретные NP-проблемы настолько же трудны, как и любая проблема этого класса. Стивен Кук (Steven Cook) доказал [365], что проблема Выполнимости (Satisfiability problem, дано правильное логическое выражение, существует ли способ присвоить правильные значения входящим в него переменным так, чтобы все выражение стало истиной?) является NP-полной. Это означает, что, если проблема Выполнимости решается за полиномиальное время, то P = NP. Наоборот, если может быть доказано, что для любой проблемы класса NP не существует детерминированного алгоритма с полиномиальным временем решения, доказательство покажет, что и для проблемы Выполнимости не существует детерминированного алгоритма с полиномиальным временем решения. В NP нет проблемы труднее, чем проблема Выполнимости.
С тех пор, как основополагающая работа Кука была опубликована, было показано, что существует множество проблем, эквивалентных проблеме Выполнимости, сотни их перечислены в [600], ряд примеров приведен ниже. Из-за эквивалентности я полагаю, что эти проблемы также являются NP-полными, они входят в класс NP и так же сложны, как и любая проблема класса NP. Если бы была доказана их решаемость за детерминированное полиномиальное время, вопрос P против NP был бы решен. Вопрос, верно ли P = NP, является центральным нерешенным вопросом теории вычислительной сложности, и не ожидается, что он будет решен в ближайшее время. Если кто-то покажет, что P = NP, то большая часть этой книги станет ненужной: как объяснялось ранее многие классы шифров тривиально взламываются за недетерминированное полиномиальное время. Если P = NP, то они вскрываются слабыми, детерминированными алгоритмами.
Следующим в иерархии сложности идет класс PSPACE. Проблемы класса PSPACE могут быть решены в полиномиальном пространстве, но не обязательно за полиномиальное время. PSPACE включает NP, но ряд проблем PSPACE кажутся сложнее, чем NP. Конечно, и это пока недоказуемо. Существует класс проблем, так называемых PSPACE-полных, обладающих следующим свойством: если любая из них является NP-проблемой, то PSPACE = NP, и если любая из них является P-проблемой, то PSPACE = P.
И наконец, существует класс проблем EXPTIME. Эти проблемы решаются за экспоненциальное время. Может быть действительно доказано, что EXPTIME-полные проблемы не могут быть решены за детерминированное полиномиальное время. Также показано, что P не равно EXPTIME.
NP-полные проблемы
Майкл Кэри (Michael Carey) и Дэвид Джонсон (David Johnson) составили список более чем 300 NP-полных проблем [600]. Вот некоторые:
— Проблема путешествующего коммивояжера. Путешествующему коммивояжеру нужно посетить различные города, используя только один бак с горючим (существует максимальное расстояние, которое он может проехать). Существует ли маршрут, позволяющий ему посетить каждый голод только один раз, используя этот единственный бак с горючим? (Это обобщение проблемы гамильтонова пути - см. раздел 5.1.)
— Проблема тройного брака. В комнате n мужчин, n женщин и n чиновников (священников, раввинов, кого угодно). Есть список разрешенных браков, записи которого состоят из одного мужчины, одной женщины и одного регистрирующего чиновника. Дан этот список троек, возможно ли построить n браков так, чтобы любой либо сочетался браком только с одним человеком или регистрировал только один брак?
— Тройная выполнимость. Есть список n логических выражений, каждое с тремя переменными. Например: если (x и y) то z, (x и w) или (не z), если ((не u и не x) или (z и (u или не x))) то (не z и u) или x), и т.д. Существует ли правильные значения всех переменных, чтобы все утверждения были истинными? (Это частный случай упомянутой выше проблемы Выполнимости.)
Теория чисел
Это не книга по теории чисел, поэтому я только набросаю ряд идей, используемых в криптографии. Если вам нужно подробное математическое изложение теории чисел, обратитесь к одной из этих книг: [1430, 72, 1171, 12, 959, 681, 742, 420]. Моими любимыми книгами по математике конечных полей являются [971, 1042]. См. также [88, 1157, 1158, 1060].
Арифметика вычетов
Вы все учили математику вычетов в школе. Иногда ее называли "арифметикой часов". Если Милдред сказала, что она будет дома к 10:00, и опоздала на 13 часов, то когда она придет домой, и на сколько лет отец лишит ее водительских прав? Это арифметика по модулю 12. Двадцать три по модулю 12 равно 11.
(10 + 13) mod 12 = 23 mod 12 = 11 mod 12
Другим способом записать это является утверждение об эквивалентности 23 и 11 по модулю 12:
10 + 13 º 11 (mod 12)
В основном, a º b (mod n), если a = b + kn для некоторого целого k. Если a неотрицательно и b находится между 0 и n, можно рассматривать b как остаток при делении a на n. Иногда, b называется вычетом a по модулю n. Иногда a называется конгруэнтным b по модулю n (знак тройного равенства, º, обозначает конгруэнтность). Одно и то же можно сказать разными способами.
Множество чисел от 0 до n-1 образует то, что называется полным множеством вычетов по модулю n. Это означает, что для любого целого a, его остаток по модулю n является некоторым числом от 0 до n-1.
Операция a mod n обозначает остаток от a, являющийся некоторым целым числом от 0 до n-1. Эта операция называется приведением по модулю. Например, 5 mod 3 = 2.
Это определение mod может отличаться от принятого в некоторых языках программирования. Например, оператор получения остатка в языке PASCAL иногда возвращает отрицательное число. Он возвращает число между -(n-1) и n-1. В языке C оператор % возвращает остаток от деления первого выражения на второе, оно может быть отрицательным числом, если любой из операндов отрицателен. Для всех алгоритмов в этой книге проверяйте, что вы добавляете n к результату операции получения остатка, если она возвращает отрицательное число.
Арифметика остатков очень похожа на обычную арифметику: она коммутативна, ассоциативна и дистрибутивна. Кроме того, приведение каждого промежуточного результата по модулю n дает тот же результат, как и выполнение всего вычисления с последующим приведением конечного результата по модулю n.
(a + b) mod n == ((a mod n) + (b mod n)) mod n
(a - b) mod n == ((a mod n) - (b mod n)) mod n
(a * b) mod n == ((a mod n) * (b mod n)) mod n
(a * (b+c)) mod n == (((a*b) mod n) + ((a*c) mod n)) mod n
Вычисление mod n часто используется в криптографии, так как вычисление дискретных логарифмов и квадратных корней mod n может быть нелегкой проблемой. Арифметика вычетов, к тому же, легче реализуется на компьютерах, поскольку она ограничивает диапазон промежуточных значений и результата. Для k-битовых вычетов n, промежуточные результаты любого сложения, вычитание или умножения будут не длиннее, чем 2k бит. Поэтому в арифметике вычетов мы можем выполнить возведение в степень без огромных промежуточных результатов. Вычисление степени некоторого числа по модулю другого числа,
ax mod n,
представляет собой просто последовательность умножений и делений, но существуют приемы, ускоряющие это действие. Один из таких приемов стремится минимизировать количество умножений по модулю, другой - оптимизировать отдельные умножения по модулю. Так как операции дистрибутивны, быстрее выполнить возведение в степень как поток последовательных умножений, каждый раз получая вычеты. Сейчас вы не чувствуете разницы, но она будет заметна при умножении 200-битовых чисел.
Например, если вы хотите вычислить a8 mod n, не выполняйте наивно семь умножений и одно приведение по модулю:
(a * a * a * a * a * a * a * a) mod n
Вместо этого выполните три меньших умножения и три меньших приведения по модулю:
((a2 mod n)2 mod n)2 mod n
Точно также,
a16 mod n =(((a2 mod n)2 mod n)2 mod n)2 mod n
Вычисление ax, где x не является степенью 2, ненамного труднее. Двоичная запись представляет x в виде суммы степеней 2: 25 - это бинарное 11001, поэтому 25 = 24 + 23 + 20. Поэтому
a25 mod n = (a*a24) mod n = (a* a8*a16) mod n =
= (a*(( a2) 2) 2*((( a2) 2) 2) 2) mod n = (a*((( a*a2) 2) 2) 2) mod n
С продуманным сохранением промежуточных результатов вам понадобится только шесть умножений:
(((((((a2 mod n)* a)2 mod n)2 mod n)2 mod n)2 mod n)2 *a) mod n
Такой прием называется цепочкой сложений [863], или методом двоичных квадратов и умножения. Он использует простую и очевидную цепочку сложений, в основе которой лежит двоичное представление числа. На языке C это выглядит следующим образом:
unsigned long qe2(unsigned long x, unsigned long y, unsigned long n) {
unsigned long s, t, u;
int i;
s=1; t=x; u=y;
while (u) {
if(u&1) s=(s*t)%n;
u>>1;
t=(t*t)%n;
}
return(s)
}
А вот другой, рекурсивный, алгоритм:
unsigned long fast_exp(unsigned long x, unsigned long y, unsigned long N) {
unsigned long tmp;
if(y==l) return(x % N);
if (l^(x&l)) {
tmp= fast_exp(x,y/2,N);
return ((tmp*tmp)%N);
else {
tmp = fast_exp(x,(y-1)/2,N);
tmp = (tmp*tmp)%N;
tmp = (tmp*x)%N;
return (tmp);
}
}
Этот метод уменьшает количество операций, в среднем, до 1.5*k операций, где k - длина числа x в битах. Найти способ вычисления с наименьшим количеством операций - трудная проблема (было доказано, что последовательность должна содержать не меньше k-1 операций), но нетрудно снизить число операций до 1.1*k или даже лучше при больших k.
Эффективным способом много раз выполнять приведение по модулю для одного n является метод Монтгомери [1111]. Другой метод называется алгоритмом Баррета [87]. Эффективность описанного алгоритма и этих двух методов рассматривается в [210]: алгоритм, рассмотренный мною, является наилучшим для единичного приведения по модулю, алгоритм Баррета - наилучшим для малых аргументов, а метод Монтгомери - наилучшим для обычного возведения в степень по модулю. (Метод Монтгомери также использует преимущество малых показателей степени, используя прием, называющийся смешанной арифметикой.)
Операция, обратная возведению в степень по модулю n, вычисляет дискретный логарифм. Я дальше вкратце рассмотрю эту операцию.
Простые числа
Простым называется целое число, большее единицы, единственными множителями которого является 1 и оно само: оно не делится ни на одно другое число. Два - это простое число. Простыми являются и 73, 2521, 2365347734339 и 2756839-1. Существует бесконечно много простых чисел. Криптография, особенно криптография с открытыми ключами, часто использует большие простые числа (512 бит и даже больше).
Евангелос Кранакис (Evangelos Kranakis) написал отличную книгу по теории чисел, простым числам и их применению в криптографии [896]. Паула Рибенбойм (Paula Ribenboim) написала две отличных справочных работы по простым числам вообще [1307, 1308].
Дата добавления: 2021-01-26; просмотров: 553;











