Квадратичные вычеты

Если p - простое число, и a больше 0, но меньше p, то a представляет собой квадратичный вычет по модулю p, если

x² º a (mod p), для некоторых x

Не все значения a соответствуют этому требованию. Чтобы a было квадратичным вычетом по n, оно должно быть квадратичным вычетом по модулю всех простых сомножителей n. Например, если p = 7, квадратичными вычетами являются числа 1, 2, и 4:

1² = 1 º 1 (mod 7)

2² = 4 º 4 (mod 7)

3² = 9 º 2 (mod 7)

4² = 16 º 2 (mod 7)

5² = 25 º 4 (mod 7)

6² = 36 º 1 (mod 7)

Заметьте, что каждый квадратичный вычет дважды появляется в этом списке. Значений x, удовлетворяющих любому из следующих уравнений, не существует:

x² º 3 (mod 7)

x² º 5 (mod 7)

x² º 6 (mod 7)

Эти числа - 3, 5 и 6 - не являются квадратичными вычетами по модулю 7.

Хотя я этого и не делаю, несложно доказать, что когда p нечетно, существует в точности (p - 1)/2 квадратичных вычетов по модулю p, и столько же чисел, не являющихся квадратичными вычетами по модулю p. Кроме того, если a - это квадратичный вычет по модулю p, то у a в точности два квадратных корня, один между 0 и (p‑1)/2, а второй - между (p - 1)/2 и (p - 1). Один из этих квадратных корней одновременно является квадратичным остатком по модулю p, он называется главным квадратным корнем.

Если n является произведением двух простых чисел, p и q, то существует ровно (p - l)(q - 1)/4 квадратичных вычетов по модулю n. Квадратичный вычет по модулю n является совершенным квадратом по модулю n, потому что для того, чтобы быть квадратом по модулю n, вычет должен быть квадратом по модулю p и квадратом по модулю q. Например, существует одиннадцать квадратичных остатков mod 35: 1, 4, 9, 11, 15, 16, 21, 25, 29 и 30. У каждого квадратичного вычета ровно четыре квадратных корня.

Символ Лежандра

Символ Лежандра, L(a,p), определен, если a - это любое целое число, а p - простое число, большее, чем 2. Он равен 0, 1 или -1.

L(a,p) = 0, если a делится на p.

L(a,p) = 1, если a - квадратичный вычет по модулю p.

L(a,p) = -1, если a не является квадратичным вычетом по модулю p.

L(a,p) можно рассчитать следующим образом:

L(a,p) = a^(p-1)/2 mod p

Или можно воспользоваться следующим алгоритмом:

1. Если a = 1, то L(a,p) = 1

2. Если a четно, то L(a,p) = L(a/2,p) *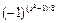

3. Если a нечетно (и ¹ 1), то L(a,p)= L(p mod a, p)*(-1)^(a-1)(p-1)/4

Обратите внимание, что этот метод также является эффективным способом определить, является ли a квадратичным вычетом по модулю p (для простого числа p).

Символ Якоби

Символ Якоби, J(a,n), представляет собой обобщение символа Лежандра на составные модули, он определяется для любого целого a и любого нечетного целого n. Функция удобна при проверке на простоту. Символ Якоби является функцией на множестве полученных вычетов делителей n и может быть вычислен по различным формулам [1412]. Вот один из способов:

Определение 1: J(a,n) определен, только если n нечетно.

Определение 2: J(0,n) = 0.

Определение 3: Если n - простое число, то символ Якоби J(a,n) = 0, если a делится на n.

Определение 4: Если n - простое число, то символ Якоби J(a,n) = 1, если a - квадратичный вычет по модулю n.

Определение 5: Если n - простое число, то символ Якоби J(a,n) = -1, если a не является квадратичным вычетом по модулю n.

Определение 6: Если n - составное число, то символ Якоби J(a,n) = J(a,p₁)* ... * J(a,p_m), где p₁, ... , p_m - это разложение n на простые сомножители.

Следующий алгоритм рекурсивно рассчитывает символ Якоби:

Правило 1: J(1,n) = 1

Правило 2: J(a*b,n) = J(a,n)* J(b,n)

Правило 3: J(2,n) =, если (n²-1) /8 нечетно, и -1 в противном случае

Правило 4: J(a,n)= J((a mod n),n)

Правило 5: J(a, b₁*b₂) = J(a, b₁)* J(a, b₂)

Правило 6: Если наибольший общий делитель a и b = 1, а также a и b нечетны:

Правило 6a: J(a,b)= J(b, a), если (a - l)(b - 1)/4 четно

Правило 6b: J(a,b)= -J(b, a), если (a - l)(b - 1)/4 нечетно

Вот алгоритм на языке C:

/* Этот алгоритм рекурсивно вычисляет символ Якоби */

int jacobi(int a, int b) {

int g;

assert(odd(b));

if (a >= b) a %= b; /* по правилу 4 */

if (a == 0) return 0; /* по определению 1 */

if (a == 1) return 1; /* по правилу 1 */

if (a < 0)

if ((b-l)/2 % 2 == 0)

return jacobi(-a,b);

else

return -jacobi(-a,b);

if (a % 2 == 0) /* a четно */

if (((b*b -1)/8) % 2 == 0)

return +jacobi(a/2,b);

else

return -jacobi(a/2,b); /* по правилам 3 и 2 */

g = gcd(a,b);

assert(odd(a)); /* это обеспечивается проверкой (a % 2 == 0) */

if (g == a) /* b делится на a */

return 0; /* по правилу 5 */

else if (g != 1)

return jacobi(g,b)*jacobi(a/g,b); /* по правилу 2 */

else if (((a-l)*(b-l)/4) % 2 == 0)

return +jacobi(b,a); /* по правилу 6a */

else

return -jacobi(b,a); /* по правилу 6b */

}

Если заранее известно, что n - простое число, вместо использования предыдущего алгоритма просто вычислите a((n-1)/2) mod n, в этом случае J(a,n) эквивалентен символу Лежандра.

Символ Якоби нельзя использовать для определения того, является ли a квадратичным вычетом по модулю n (если, конечно, n не является простым числом). Обратите внимание, что если J(a,n) = 1 и n - составное число, то утверждение, что a является квадратичным вычетом по модулю n, не обязательно будет истиной. Например:

J(7,143) = J(7,11)* J(7,13) = (-1)(-1) = 1

Однако не существует таких целых чисел x, что x² º 7 (mod 143).

Целые числа Блюма

Если p и q - два простых числа, конгруэнтных 3 по модулю 4, то n = pq иногда называют целым числом Блюма. Если n - это целое число Блюма, у каждого квадратичного вычета ровно четыре квадратных корня, один из которых также является квадратом - это главный квадратный корень. Например, главный квадратный корень 139 mod 437 - это 24. Остальные три корня - это 185, 252 и 413.

Генераторы

Если p - простое число, и g меньше, чем p, то g называется генератором по модулю p, если для каждого числа b от 1 до p - 1 существует некоторое число a, что g^a º b (mod p).

Иными словами, g является примитивом по отношению к p. Например, если p = 11, то 2 - это генератор по модулю 11:

2¹⁰ = 1024 º 1 (mod 11)

2¹ = 2 º 2 (mod 11)

2⁸ = 256 º 3 (mod 11)

2² = 4 º 4 (mod 11)

2⁴ = 16 º 5 (mod 11)

2⁹ = 512 º 6 (mod 11)

2⁷ = 128 º 7 (mod 11)

2³ = 8 º 8 (mod 11)

2⁶ = 64 º 9 (mod 11)

2⁵ = 32 º 10 (mod 11)

Каждое число от 1 до 10 может быть представлено как 2^a (mod p). Для p = 11 генераторами являются 2, 6, 7 и 8. Другие числа не являются генераторами. Например, генератором не является число 3, потому что не существует решения для

3^a º 2 (mod 11)

В общем случае проверить, является ли данное число генератором, нелегко. Однако задщача упрощается, если известно разложение на множители для p - 1. Пусть q₁, q₂, ... , q_n - это различные простые множители p - 1. Чтобы проверить, является ли число g генератором по модулю p, вычислите

g^(p-1)/q mod p

для всех значений q = q₁, q₂, ... , q_n.

Если это число равно 1 для некоторого q, то g не является генератором. Если для всех значений q рассчитанное значение не равно 1, то g - это генератор.

Например, пусть p = 11. Простые множители p - 1 = 10 - это 2 и 5. Для проверки того, является ли число 2 генератором, вычислим:

2^(11-1)/5 (mod 11) = 4

2^(11-1)/2 (mod 11) = 10

Ни один из ответов не равен 1, поэтому 2 - это генератор.

Проверим, является генератором ли число 3:

3^(11-1)/5 (mod 11) = 9

3^(11-1)/2 (mod 11) = 1

Следовательно, 3 - это не генератор.

При необходимости обнаружить генератор по модулю p просто случайно выбирайте число от 1 до p - 1 и проверяйте, не является ли оно генератором. Генераторов достаточно, поэтому один из них вы, скорее всего, найдете быстро.