Вычитая первое уравнение из второго, получим

ΔG = RT( ln П – ln K_N).

Это уравнение называется изотермой химической реакции и позволяет предсказать направление реакции.

Если δG < 0, то реакция идет вправо;

δG > 0, то реакция идет влево.

В частном случае

N_AB→0; П→ ∞; ln П → – ∞.

Реакция пойдет в сторону образования АВ.

Равновесие в гетерогенных системах. Правило фаз

Гетерогенной называется система, состоящая из отдельных частей, ограниченных физическими поверхностями раздела (фаз). Гетерогенные системы могут быть построены из нескольких веществ (многокомпонентные) и из одного вещества – многокомпонентные.

Число компонентов К равно разности между числом веществ в системе и количеством независимых реакций между ними. Рассмотрим пример.

СО2

СаО

СаСО3

СаСО₃ ↔ СаО + СО₂

Достаточно знать только два вещества, а третье получится из уравнения реакции : К=3-1=2.

Число компонентов–количество различных видов молекул, необходимых для построения данной системы.

Общее условие равновесия гетерогенных систем – равновесие между отдельными частями системы (фазами).

Параметры гетерогенной системы: температура Т, давление р и концентрация всех компонентов во всех фазах, если они имеют сложный состав.

Условие равновесия прежнее:

ΔG → 0; G → min.

Однако условие равновесия зависит также и от строения системы (числа фаз Ф и числа компонентов К), при этом устанавливаются связи между параметрами равновесия, причем некоторые параметры остаются свободными, т.е. могут изменяться без изменения строения системы (числа фаз). Это соотношение отражает правило фаз Гиббса – Коновалова:

С=К-Ф+2, где С – число степеней свободы.

Пример 1: СаСО₃ ↔ СаО + СО₂ .Здесь К=2, Ф=3, С=1.

Система моновариантная – давление является функцией температуры

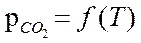
Пример 2. FeO_тв + СО ↔ Fe_тв + СО₂

Число фаз – 3, число компонентов – 3, С=2.

Система бивариантная, параметры равновесия – Т, р и х.

p_СО = f(T,x) .

Пример 3. Нонвариантная система «лед + вода + пар»

Тройная точка воды.