Расчет координат промежуточных точек ортодромии
1) По значениям λ0 и К0.
λ0 = 97°29,6′W К0 = 47°47,6′.
| По формуле 26.7 → | tgφi = sin(λi − λ0) · ctg К0 |
из табл. 6а «МТ-75» (с. 155÷199) или табл. 5.42а «МТ-2000» (с. 460÷461).
Для промежуточной точки № 1:
tgφi = sin(λi − λ0) · ctg К0 = sin(67°29,6′ − 97°29,6′) · ctg47°47,6′ = sin30° · ctg47°47,6′ = 0,50000 · 0,90685 = 0,45343(tgφi) →
→ из табл. 6а «МТ-75» или табл. 5.42а «МТ-2000» (обратный вход) →
φi = 24°23,6′N (см. табл. 26.6).
Задаваясь значениями долготы λi (через 10°) по формуле (7) рассчитываем значения широт всех промежуточных точек φi. Выполним это через логарифмы (табл. 26.2):
lg tgφi = lg sin(λi − λi) + lg ctg K0
табл. 5а «МТ-75» (с. 93÷137) (табл. 26.7).
Таблица 26.2
| №№ точек | Заданная долгота λi (через 10°) | λi − λ0 λ0 = 97°29,6′W | lg sin(λi − λ0) |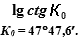 
| lg tgφi | φi |
| 67°29,6′W | 30° | 9,69897 | 9,95759 | 9,65656 | 24°23,6′N | |
| 57°29,6′W | 40° | 9,80807 | 9,95759 | 9,76566 | 30°14,5′N | |
| 47°29,6′W | 50° | 9,88425 | 9,95759 | 9,84184 | 34°47,4′N | |
| 37°29,6′W | 60° | 9,93753 | 9,95759 | 9,89512 | 38°08,9′N | |
| 27°29,6′W | 70° | 9,97299 | 9,95759 | 9,93058 | 40°26,4′N | |
| 17°29,6′W | 80° | 9,99335 | 9,95759 | 9,95094 | 41°46,2′N |
2) Проверим правильность расчета φi по координатам «вертекса»
φV = 90° − K0 = 90° − 47°47,6′ = 42°12,4′N
λV = λ0±90° = 97°29,6′ − 90° = 7°29,6′W
tgφi = cosθi · tgφV
| θ = λV − λi | (26.16) |
| lgφi = lg cosθi + lg tgφV | (26.17) |
табл. 5а «МТ-75» (с. 93÷137).
Для промежуточной точки № 1:
tgφi = cos(λV − λi) · tgφV = cos(7°29,6′ − 67°29,6′) · tg42°12,4′ = cos60° · tg42°12,4′ = 0,50000 · 0,90695 = 0,4534(tgφi) →
→ из табл. 6а «МТ-75» или табл. 5.42а «МТ-2000» (обратный вход) →
φi = 24°23,6′N (см. табл. 26.6).
Задаваясь значениями долготы λi через 10° (λ2 = 57°29,6′W, λ3 = 47°29,6′W, λ4 = 37°29,6′W, λ5 = 27°29,6′W, λ6 = 17°29,6′W) по формуле (26.17) рассчитываем значения широт всех промежуточных точек. Выполним это через логарифмы по формуле (26.17). Результаты расчетов сведены в табл. 26.3.
Таблица 26.3
| №№ точек | Заданная долгота λi (через 10°) | θ = λV − λi λV = 7°29,6′W | lg cosθ | lg tgφV (φV = 42°12,4′N) | lg tgφi | φi |
| 67°29,6′W | 60° | 9,69897 | 9,95758 | 9,65655 | 24°23,6′N | |
| 57°29,6′W | 50° | 9,80807 | 9,95758 | 9,76565 | 30°14,5′N | |
| 47°29,6′W | 40° | 9,88425 | 9,95758 | 9,84183 | 34°47,4′N | |
| 37°29,6′W | 30° | 9,93753 | 9,95758 | 9,89511 | 38°08,9′N | |
| 27°29,6′W | 20° | 9,97299 | 9,95758 | 9,93057 | 40°26,4′N | |
| 17°29,6′W | 10° | 9,99335 | 9,95758 | 9,95093 | 41°46,2′N |
| Вывод: | расчеты выполнены правильно. Аналогично можно выполнить расчет φi через 5° по долготе (а не через 10°), что чаще всего и выполняется. |
Нанеся по координатам начальную точку (т. А), 6 промежуточных точек (тт. 1÷6) и конечную точку (т. В) на морскую навигационную карту(ы), получим (рис. 26.6) маршрут перехода судна с изменением курса через каждые 10° долготы (плавание по хордам ортодромии).
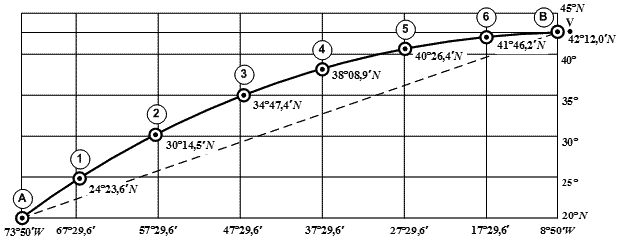
Рис. 26.6. Схема плавания судна по хордам ортодромии
Дата добавления: 2021-01-26; просмотров: 417;
Поиск по сайту
Узнать еще
- A. Узагальнені координати і узагальнені швидкості та прискорення
- B). Система относительных координат.
- E) Расчет структурных составляющих очага деформации с одним нейтральным сечением
- I. Погрешности механической обработки. Точность обработки. Методы их расчёта
- IV. РАСЧЕТ РЕКТИФИКАЦИОННЫХ КОЛОНН
- V. ПРИМЕР РАСЧЕТА ФИЛЬТРА ВЫСОКИХ ЧАСТОТ ЧЕБЫШЕВА
- А) Расчет электрической цепи методом свертывания
- А. Расчет на устойчивость
Публикации по технике и механике
Публикации по биологии
Публикации по информатике
Публикации по строительству
Публикации по физике
Публикации по химии
Публикации по электронике
Публикации по искусству
Публикации по истории
