Основные формулы ортодромии
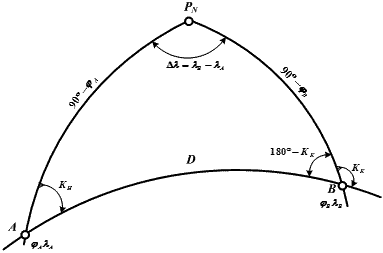
Рис. 26.4. Сферический треугольник ортодромии
Треугольник АРNВ – сферический треугольник, элементами которого являются (рис. 26.4):
- Стороны треугольника АРNВ:
- АРN → (90° – φA);
- РNВ → (90° – φB);
- АВ → D (длина ортодромии)
- Углы треугольника АРNВ:
-
 РNАВ → КH (начальный курс плавания по ДБК);
РNАВ → КH (начальный курс плавания по ДБК); -
 РNВА → 180° – КK (конечный курс плавания по ДБК);
РNВА → 180° – КK (конечный курс плавания по ДБК); -
 АРNВ → Δλ = λB – λA (разность долгот между конечной В и начальной А точками ДБК).
АРNВ → Δλ = λB – λA (разность долгот между конечной В и начальной А точками ДБК).
Из сферической тригонометрии известно «…если в сферическом треугольнике известны три элемента то, по формулам сферической тригонометрии, можно определить и все остальные…».
Применяя формулу «косинуса стороны» («…косинус стороны равен произведению косинусов двух других сторон плюс произведение синусов тех же сторон на косинус угла между ними…») можно определить длину ортодромии (D) между любыми двумя ее точками (т. А и т. В), координаты которых известны, то есть:
cosD = cos(90° − φA) · cos(90° − φB) + sin(90° − φA) · sin(90° − φB) · cos(λB – λA)
или, после преобразования:
| cosD = sinφA · sinφB + cosφA · cosφB · cos(λB – λA) | (26.3) |
Применяя формулу «котангенса угла» («…произведение котангенса крайнего угла на синус среднего угла равно произведению котангенса крайней стороны на синус средней стороны минус произведение косинусов средних частей…») можно определить значение начального КH и конечного КK курсов плавания по ортодромии.
| ctgКH = cosφA · tgφB · cosec(λB – λA) − sinφA · ctg(λB – λA) | (26.4) |
| ctgКK = −tgφA · cosφB · cosec(λB – λA) + sinφB · ctg(λB – λA) | (26.5) |
Аналогично определяем остальные величины:
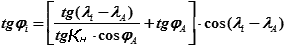
| (26.6) |
или
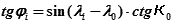
| (26.7) |
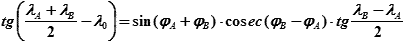
| (26.8) |
| tgφi = cosθi · tgφV | (26.9) |
где θ = λV − λi.
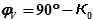
| (26.10) |
| λV = λ0 ± 90° | (26.11) |
Дата добавления: 2021-01-26; просмотров: 775;











