Расчет пройденного по ортодромии расстояния (D)
По формуле 26.3:
| cos D | = | sin φA · sin φB + cos φA · cos φB · cos (λB – λA) |
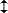
| +20°00′ +42°12′ +20°00′ +42°12′ +65°00′ из табл. 6а «МТ-75» (с. 155÷199) или табл. 5.42а «МТ-2000» (с. 460÷461): | |
0,52394 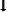
| = | 0,34202 · 0,67172 + 0,93969 · 0,74080 · 0,42262 из табл. 6а «МТ-75» (или табл. 5.42а «МТ-2000») обратным входом |
| ≈ 58°24,2′ = 3504,2 мили → D. (58° · 60′ + 24,2′) → см. табл. 26.6. |
Расчет расстояния D, выполненный по формуле (26.3), проверяем решением данной задачи по таблицам «ТВА-57», где (см. табл. 26.1).
a. вместо δ → φB;
b. вместо t → РД;
c. вместо φC → φA.
Решение по «ТВА-57» возможно, если D < 5400 миль:
Таблица 26.1.

Вывод: и по формуле и по «ТВА-57» – D = 3504,3 мили.
Оцениваем экономичность плавания по ортодромии.
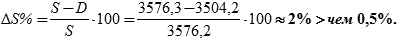
Вывод: плавание по ортодромии выгодно.
26.4.2. Расчет начального курса плавания по ортодромии (КH)
По формуле 26.4:
| ctg КH | = | cos φA · tg φB · cosec (λB – λA) – sin φA · ctg (λB – λA) |
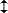
| +20°00′ +42°12′ +65°00′ +20°00′ +65°00′ из табл. 6а «МТ-75» (с. 155÷199) или табл. 5.42а «МТ-2000» (с. 460÷461): | |
0,78064 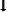
| = | 0,93969 · 0,90674 · 1,10338 – 0,34202 · 0,46631 из табл. 6а «МТ-75» (или табл. 5.42а «МТ-2000») обратным входом |
| КH = 52°01,4′ ≈ 52,0° (см. табл. 26.6). |
| Вывод: | и по «ТВА-57» и по формуле – начальный курс плавания по ортодромии из т. А → КH = 52°01,4′ ≈ 52,0°. |
Правило знаков:
- Если φN, то все функции «+»;
- Если φS, то sin «–», а cos «+»;
- Знак cosΔλ зависит лишь от величины угла, но не зависит от его наименования (Δλ < 90° → cos «+» и наоборот).
26.4.3. Расчет конечного курса плавания по ортодромии (КK)
По формуле 26.5:
| ctg КK | = | –tg φA · cos φB · cosec (λB – λA) + sin φB · ctg (λB – λA) |
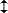
| +20°00′ +42°12′ +65°00′ +42°12′ +65°00′ из табл. 6а «МТ-75» (с. 155÷199) или табл. 5.42а «МТ-2000» (с. 460÷461): | |
0,01573 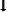
| = | –0,36397 · 0,74080 · 1,10338 + 0,67172 · 0,46631 из табл. 6а «МТ-75» (или табл. 5.42а «МТ-2000») обратным входом по ctg КK = 0,01573 находим значение |
| КK = 89°06,0′ ≈ 89,1°, т.е. в т. В курс судна КK = 89,1° (см. табл. 26.6). |
26.4.4. Расчет значений К0 и λ0
По формуле 26.8:
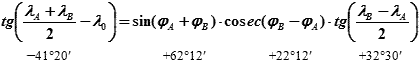
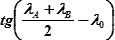 = sin62°12′ · cosec22°12′ · tg32°30′ = (см. т. 6а «МТ-75» или т. 5.42а «МТ-2000») = 0,88458 · 2,64662 · 0,63707 = 1,49147
= sin62°12′ · cosec22°12′ · tg32°30′ = (см. т. 6а «МТ-75» или т. 5.42а «МТ-2000») = 0,88458 · 2,64662 · 0,63707 = 1,49147
т.е.
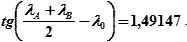
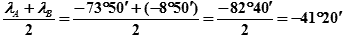
tg(−41°20′ − λ0) = (т. 6а «МТ-75» или т. 5.42а «МТ-2000») = 56°09,6′ (см. табл. 26.6).
Тогда:
−41°20′ − λ0 = 56°09,6′,
а для
λ0 = −41°20′ − 56°09,6′ = −97°29,6′
т.е.
| λ0 = 97°29,6′W. |
(Или через логарифмы):
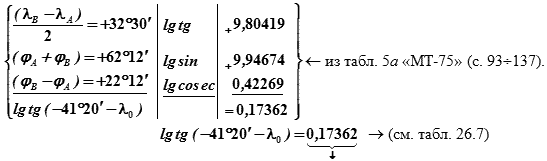
из табл. 5а «МТ-75» (с. 93÷137) обратным входом → 56°09,6′ и тогда:
λ0 = −41°20,0′ − 56°09,6′ = −97°29,6′
т.е.
| λ0 = 97°29,6′W. |
А по формуле (26.7):
tgφA = sin(λA − λ0) · ctgK0
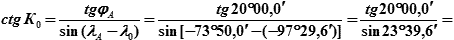

(Или через логарифмы):
| + lg tg φA | (+20°00′) | = | 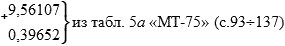
|
| lg cosec (λA – λ0) | (+23°39,6′) | = | |
| = lg ctg К0 → | = 9,95759 → из т. 5а «МТ-75» (обратным входом) → 47°47,6′ ≈ 47,8°, т.е. К0 = 47,8° (см. табл. 26.7). |
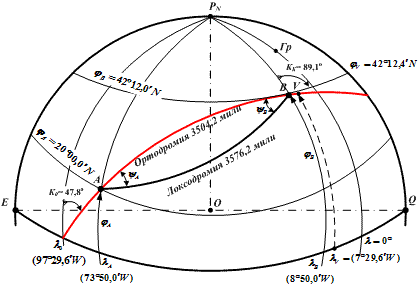
Рис. 26.5. Схема плавания судна по ДБК – ортодромии
Дата добавления: 2021-01-26; просмотров: 765;











