Построение меркаторской карты
Для построения меркаторской карты необходимо знать:
1.
| → ее границы: | 
| φN и φS − широту ее северной и южной рамки; |
| λE(W) и λE(W) − долготу ее восточной и западной рамки; |
2. → главную параллель карты (φ0), значение которой зависит от района:
· для Балтийского моря – φ0 = 60°;
· для Белого моря – φ0 = 66°;
· для Черного моря – φ0 = 44°;
· для открытых частей океанов и морей введены широтные полосы с главной параллелью 0°, 25°, 30°, 40°; и т.д.
3. → масштаб по главной параллели или главный масштаб карты (μ0), который показывает, во сколько раз уменьшено изображение земной поверхности вдоль конкретной (главной) параллели при ее проектировании.
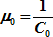
| (6.16) |
4. где С0 – знаменатель главного масштаба (указан в заголовке карты).
5. → интервалы нанесения на карту параллелей (Δφ) и меридианов (Δλ).
Для расчета карты используются следующие простые формулы (рис. 6.4):
| (6.17) |
| где | е – единица карты – длина одной минуты дуги параллели, выраженная в мм в масштабе карты (ф 6.15); |
где:
| p0 = a · cosU0 · arc1′ | (6.18) |
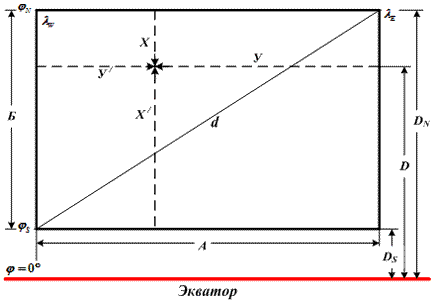
Рис. 6.4. Построение Меркаторской карты
а = 6 378 245 м;
U0 = φ0 – Δφ – приведенная широта главной параллели;
Δφ = 5,76′ · sin 2φ0;
DN, DS – меридиональные части северной и южной рамки карты, выбираемые из Картографических таблиц (КТ) или табл. 26 «МТ-75» (с. 280÷287) или табл. 2.28а «МТ-2000» (с. 314÷321).
Для шара:
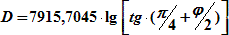
| (6.19) |
* В КТ (картографических таблицах) приведены готовые значения единиц карты (е) для всех стандартных масштабов.
Для проверки графических построений может быть вычислена диагональ d рамки карты
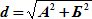
| (6.20) |
Для контроля рассчитывают положение параллелей и от северной и от южной рамок карты:
| (6.21) |
С той же целью определяют положение меридианов и от восточной и от западной рамок карты:
| (6.22) |
Разности меридиональных частей (РМЧ) и разности долгот рассчитывают в экваториальных минутах.
Контролирующие суммы вычисляют так:
| (6.23) |
В случае, когда интервал между параллелями, полученный по формуле:
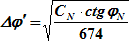
| (6.24) |
не превышает Δφ′, разбивку сторон рамки между ними можно производить путем линейной интерполяции.
СN – знаменатель частного масштаба.
Частный масштаб меркаторской карты – масштаб на какой-либо заданной параллели φ.
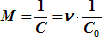
| (6.25) |
| где | ν – модуль параллели – отношение длины 1′ дуги главной параллели в проекции Меркатора к длине 1′ дуги параллели заданной широты: |
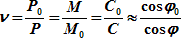
| (6.26) |
| где | C0 = ν · C → знаменатель главного масштаба М0 = 1/С0 |
| C = C0/ν → знаменатель частного масштаба М = 1/С. |
Увеличение масштаба – во сколько раз отличается масштаб на какой-либо параллели от масштаба на главной параллели.
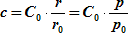
| (6.27) |
| где | r (r0) – радиус какой-либо (главной) параллели; |
| р (р0) – длина одной минуты дуги какой-либо (главной) параллели в мм на широте φ | |
| φ (φ0) – дается в КТ. |
Меркаторская миля – длина изображения одной минуты дуги меридиана (Δφ) в проекции Меркатора, выраженная в линейных единицах в масштабе карты.
1 меркаторская миля = 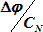
| (6.28) |
где СN – знаменатель частного масштаба на данной широте.
1 меркаторская миля (см) = 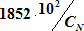
| (6.29) |
Линейный морской масштаб (lφ) – величина, которая показывает, сколько морских миль содержится в 1 см карты, и представляет величину, обратную меркаторской миле.
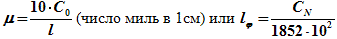
| (6.30) |
где l → длина 1′ дуги меридиана (в мм) для главной параллели (φ0).
Например: для φ0 = 60° → e = 1,002.674 (из табл. 6.3) · 1852.000 = 1.856.902.
Дата добавления: 2021-01-26; просмотров: 641;