Задача № 2. Расчет счислимого места судна на заданный момент времени.
Нахождение счислимого места на заданный момент времени сводится к построению треугольника перемещений (ΔОСД) подобного навигационному скоростному треугольнику (ΔОАБ).
Дано: Т0 (09.50), ОЛ0 (33,0), ГКК (96,0°), ΔГК (–1,0°), β (–5,0°), V0 (7,0 уз.), КТ (50,0°), υТ (1,4 уз.).
Найти: счислимое место судна на момент времени Т1 (11.10) при ОЛ1 (42,7).
Решение (рис. 8.12):
1. → Выполняем пп. 1÷6 по задаче № 1.
2. → Рассчитываем пройденное судном расстояние от исходной точки (т. О) до заданного 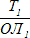 :
:
a. РОЛ = ОЛ1 − ОЛ0 = 42,7 − 33,0 = 9,7;
b. SЛ = КЛ · РОЛ = 0,96 · 9,7 = 9,3(КЛ – из «Таблицы поправок лага по VЛ = 7,0 уз.);
c. SОБ = VОБ · t = 7,0 · 1ч 20м = 9,3,где t = Т1 – Т0 = 11.10 – 09.50 = 1ч 20м. SЛ = SОБ.
3. → Рассчитанное расстояние SЛ = SОБ (9,3 мили) отложим от исходной точки (т. О) по линии истинного курса (ИК) – (SЛ = SОБ = 9,3 мили – 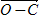 ).
).
4. → Из полученной на линии ИК точки (т. С) проводим линию по направлению учитываемого течения КТ ( 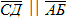 ) до пересечения ее с линией пути на течении. Точка пересечения (т. Д) и даст нам искомое счислимое место судна на заданный момент времени.
) до пересечения ее с линией пути на течении. Точка пересечения (т. Д) и даст нам искомое счислимое место судна на заданный момент времени.
5. → У счислимого места на заданный момент времени (т. Д) подписываем 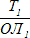
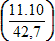 .
.
| Задача № 3. | Предвычисление времени и отсчета лага прихода судна в заданную точку при учете течения. |
Точка, как правило, задается: 1. координатами (φ, λ); 2. Направлением на ориентир (пеленг или курсовой угол); 3. Расстоянием до ориентира.
Независимо от способа «задания» точки, она должна находиться на линии пути при учете течения (ПУβ) → т. «Д».
Дано: ГКК (92,0°), ΔГК (–2,0°), V0 (7,0 уз.), КТ (145,0°), υТ (2,0 уз.).
Найти: 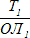 , когда судно будет в заданной точке Д (φ и λ;
, когда судно будет в заданной точке Д (φ и λ; 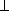 ор. К; DЗ ор. М).
ор. К; DЗ ор. М).
Решение (рис. 8.13):
1. → Выполняем пп. 1÷6 по задаче № 1 (ПУβ = 103,0°, β = +13,0°).
2. → Находим место заданной т. Д на карте (1. по φ и λ; 2. по 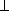 ор. К – ИК
ор. К – ИК  = ИК – 90° = 0,0° или с ор. К на судно – ОИП° = 180,0°; 3. по DЗ от ор. М).
= ИК – 90° = 0,0° или с ор. К на судно – ОИП° = 180,0°; 3. по DЗ от ор. М).
3. → Из т. Д проводим линию, обратную направлению течения (КТ ±180°), до пересечения ее с линией истинного курса судна ИК ( 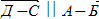 ) → т. С.
) → т. С.
4. → С помощью циркуля-измерителя снимаем расстояние (S) от т. О до т. С по линии истинного курса судна (ИК).
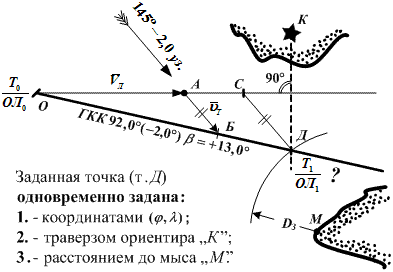
Рис. 8.13. Предвычисление времени и отсчета лага прихода судна в заданную точку при учете течения
5. → Рассчитываем время (Т1) и отсчет лага (ОЛ1):
T1 = T0 + t, где 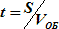 и ОЛ1 = ОЛ0 + РОЛ, где
и ОЛ1 = ОЛ0 + РОЛ, где 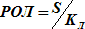 (S ~
(S ~ 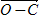 ).
).
6. → Подписываем найденные значения 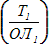 у заданной точки (т. Д).
у заданной точки (т. Д).
| Задача № 4. | (обратная № 1) Расчет компасного или истинного курса по известным элементам течения (КТ, υТ), скорости судна (V0) и заданной линии пути при течении (ПУβ). |
Дано: ПУβ (путь к причалу), V0, КТ, υТ.
Найти: КК, β.
Решение (рис. 8.14):
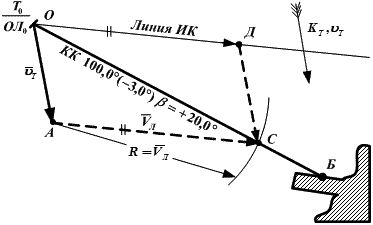
Рис. 8.14. Расчет компасного курса судна при учете течения
1. → Из точки начала учета течения (т. О) проводим заданную линию пути при течении – ПУβ ( 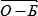 ) 117,0°. → ее направление снимаем с карты.
) 117,0°. → ее направление снимаем с карты.
2. → Из этой же точки (т. О) проводим линию по направлению течения ( 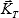 ) и отложим на ней (от т. О) вектор скорости течения
) и отложим на ней (от т. О) вектор скорости течения 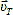 в масштабе карты.
в масштабе карты.
3. → Из конца вектора течения 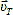 (т. А) радиусом, равным скорости судна
(т. А) радиусом, равным скорости судна 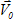 (в том же масштабе) делаем засечку на линии пути при течении → т. С.
(в том же масштабе) делаем засечку на линии пути при течении → т. С.
4. → С помощью параллельной линейки соединяем конец вектора течения 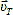 (т. А) и т. С и параллельно переносим в точку начала учета течения (т.е.
(т. А) и т. С и параллельно переносим в точку начала учета течения (т.е.  ). Направление линий
). Направление линий 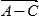 и
и 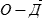 соответствует истинному курсу (ИК) судна. С помощью параллельной линейки и транспортира штурманского снимаем направление линии истинного курса судна (ИК = 97,0°).
соответствует истинному курсу (ИК) судна. С помощью параллельной линейки и транспортира штурманского снимаем направление линии истинного курса судна (ИК = 97,0°).
5. → Рассчитываем значение угла сноса судна течением:
β = ПУβ − ИК = 117,0° − 97,0° = +20,0°.
6. → Рассчитываем значение гирокомпасного курса судна:
ГКК = ИК − ΔГК = 97,0° − (− 3,0°) = 100,0°.
(этот курс рулевой будет держать по компасу от т. О до т. Б).
7. → Заполняем по форме судовой журнал.
Примечание:
Задачу № 4 обычно называют «обратной задачей при учете течения», а задачу № 1 → «прямой задачей при учете течения».
Дата добавления: 2021-01-26; просмотров: 635;











