Лекция 3: Высказывания и высказывательные формы.

Понятие функции. Способы задания функции.

Определение

Функциональной зависимостью называют такую зависимость, для которой указано правило, с помощью которого для каждого значения независимой переменной (аргумента) можно найти единственное значение зависимой переменной (значение функции).

Независимую переменную (аргумент функции) обычно обозначают x. Зависимую переменную (значение функции) обычно обозначают y.

Наиболее распространенные три способа задания функции: табличный, графический, аналитический, существуют еще словесный и рекурсивный способы.

1. Табличный способ наиболее широко распространен (таблицы логарифмов, квадратных корней), основное его достоинство – возможность получения числового значения функции, недостатки заключаются в том, что таблица может быть трудно читаема и иногда не содержит промежуточных значений аргумента. При табличном способе задания функции в одной строке таблицы записывают значения аргумента, а в другой — соответствующее каждому аргументу значение функции.

Например:

Аргумент х принимает заданные в таблице значения, а Y определяется соответственно этому аргументу X.

2. Графический способнаглядно представляет функциональную зависимость. Чтобы графически задать функцию Y(X), надо на координатной плоскости отметить все точки (a;b) такие, что Y(a)=b. Полученная линия называется графиком функции.Часто для наглядности масштабы на осях принимают разными. Заметим, что координатные оси тоже принято обозначать X и Y. Это не случайное совпадение, по оси Ox откладывается значение аргумента, а по оси Oy − значение функции.

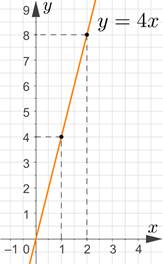
Рис.1

На рисунке 1 представлен график функции y=4x. Он проходит через точки (0;0),(1;4),(2;8), так как y(0)=0,y(1)=4,y(2)=8.

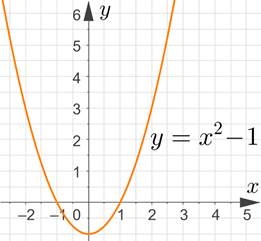Рис. 2

На рисунке 2 представлен график функции y=X^2−1

Достоинства этого способа задания функций заключаются в легкости и целостности восприятия, в непрерывности изменения аргумента; недостатком является уменьшение степени точности и сложность получения точных значений.

3. Аналитический способсостоит в задании функции одной или несколькими формулами. Основным достоинством этого способа является высокая точность определения функции от интересующего аргумента, а недостатком является затрата времени на проведение дополнительных математических операций.

Например:

Функцию можно задать с помощью математической формулы Y=X², тогда если X равно 2, то Y равно 4, возводим X в квадрат.

Однако не любая формула задаёт функцию. Например, формула |Y|=X функцию не задаёт, так как значению аргумента X сопоставляется не единственное значение Y, а целых два значения функции: Y и −Y.

Понятие отношения на множестве. Свойства отношений. (есть) (На 1 сессии)

Лекция 3: Высказывания и высказывательные формы.

Взаимосвязи между объектами и свойствами выражаются с помощью предложений. Предложения могут быть сформулированы при помощи слов и записаны при помощи математических символов:

«У квадрата все стороны равны»; «5 <7». Каждое математическое предложение характеризуется содержанием и логической структурой.

По структуре различают элементарные и составныепредложения.

Элементарные: 1) «20 – четное число»; 2) «х> 8».

Составные: 1)" 20 четное и делится на 5 «; 2) «х 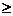8»,

Составные предложения образуются из элементарных с помощью слов "и", "или", частицы "не". Эти слова называются логическими связками.

Пример: " 20 четное и делится на 5 "

Логическая структура: «А и В», где А - "20 четное число", В -"20 делится на 5"

Среди предложений выделяют высказывания и высказывательные формы.

Определение. Высказыванием называется повествовательное предложение, о котором можно сказать истинно оно или ложно.

Высказывания обычно обозначают большими латинскими буквами. Если высказывание А истинно, то записывают: А – «и» или присваивают А значение 1, если высказывание А ложно, то пишут А – «л» или А имеет значение 0. «Истина» и «ложь» называются значениями истинности высказываний. Например, предложение «Саратов расположен на берегу реки Волги» является высказыванием, причем истинным высказыванием. Предложение «Число 25 делится на 3» – ложное высказывание. Выражение «25 + 6» высказыванием не является, так как о нем нельзя сказать истинно оно или ложно. Не являются высказываниями предложения, содержащие переменную величину, например: «Число х больше числа 8».

Слова «неверно, что», «и», «или», «если … , то», «тогда и только тогда, когда» называются логическими связками.

Высказывания делятся на простые (элементарные) и составные. Составные высказывания содержат логические связки и могут быть разбиты на простые высказывания. Например, высказывание «6 > 3» является простым, а высказывание «5 < 8 < 12» является составным, так как его можно разбить на два простых высказывания: «5 < 8» и «8 < 12».

Определение.Высказывательной формой или предикатом называется предложение с одной или несколькими переменными, обращающееся в высказывание, если вместо переменных подставить их значения.

По числу переменных, входящих в предикат, различают одноместные, двухместные и т. д. предикаты и обозначают: А( х ), А( х , у ) и т. д. Например, х + 5 = 9 – одноместный предикат, а предложение «Число х делится на число у » – двухместный.

П р и м е р 1. Выясните, какие из следующих предложений являются высказываниями, а какие предикатами: а) 452 < 237; б) 5 х – 6 = 4; в) Сколько стоит эта книга?; г) Число кратно 7?

Р е ш е н и е.

а) Предложение 452 < 237 является высказыванием, так как можно утверждать, что оно ложно.

б) Предложение 5 х – 6 = 4 является предикатом, так как это предложение содержит переменную х и при подстановке конкретного значения х превращается в высказывание. Если х = 3 , то 5·3 – 6 = 4 – ложное высказывание, если х = 2, то 5·2 – 6 = 4 – истинное высказывание.

в) Предложение «Сколько стоит эта книга?» не является высказыванием, так как о вопросительных предложениях бессмысленно ставить вопрос об их истинности или ложности. Данное предложение не является и предикатом.

г) Несмотря на то, что в предложении «Число кратно 7» переменная не содержится в явном виде, ее наличие подразумевается, поэтому данное предложение является предикатом. Оно превращается в высказывание при подстановке в него конкретного числа.