Умозаключения и их виды

Умозаключение - это способ получения нового знания на основе некоторого имеющегося. При этом не обращаемся к исследованию предметов и явлений самой действительности, а открываем связи и отношения между ними, которые невозможно увидеть непосредственно.
Умозаключение состоит из посылок и заключения.
Посылки - это высказывания, содержащие исходное знание.
Заключение - это высказывание, содержащее новое знание, полученное из исходного.
В умозаключении из посылок выводится заключение.

Умозаключения делятся на три вида:

1)Дедуктивные умозаключения – это умозаключения, в которых из общего правила делается вывод для частного случая (из общего правила выводится частный случай).

2)Индуктивные умозаключения - это умозаключения, в которых из нескольких частных случаев выводится общее правило (несколько частных случаев как бы наводят на общее правило

3)Умозаключения по аналогии – это умозаключения, в которых на основе сходства предметов (объектов) в одних признаках делается вывод об их сходстве и в других признаках.

В логике вместо термина «рассуждения» чаще используются (как его синоним) слово «умозаключение», им и будем пользоваться.

Умозаключение - это способ получения нового знания на основе некоторого имеющегося. При этом мы не обращаемся к исследованию предметов и явлений самой действительности, а открываем такие связи и отношения между ними, которые невозможно увидеть непосредственно.

Умозаключение состоит из посылок и заключения.

Посылки - это высказывания, содержащие исходное знание.

Заключение - это высказывание, содержащее новое знание, полученное из исходного. В умозаключении из посылок выводится заключение.

Рассмотрим примеры умозаключений, которые выполняют младшие школьники, изучая математику.

П р и м е р 1. Ученику предлагается объяснить, почему число 23 можно представить в виде суммы 20 + 3. Он рассуждает: Число 23 - двузначное. Любое двузначное число можно представить в виде суммы разрядных слагаемых. Следовательно, 23 = 20 + 3».

Первое и второе предложения в этом умозаключении посылки, причем одна посылка общего характера - это высказывание «любое двузначное число можно представить в виде суммы разрядных слагаемых», а другая - частная, она характеризует только число 23 - оно двузначное. Заключение - это предложение, которое стоит после слова «следовательно», - также носит частный характер, так как в нем речь идет о конкретном числе 23.

П р и м е р 2. Один из приемов ознакомления младших школьников с переместительным свойством умножения заключается в следующем. Используя различные средства наглядности, школьники вместе с учителем устанавливают, что 6·3 = 3·6, 5·2 = 2·5, 3·7 = 7·3. А затем, на основе полученных равенств делают вывод: для всех натуральных чисел а и b верно равенство ab = ba.

В данном умозаключении посылками являются первые три равенства, в них утверждается, что для конкретных натуральных чисел выполняется такое свойство. Заключением в данном примере является утверждение общего характера - переместительное свойство умножения натуральных чисел.

П р и м е р 3. При обучении делению на однозначное число используется такой прием. Сначала выясняется: чтобы найти значения высказывания 12:4, следует узнать, на какое число надо умножить делитель 4, чтобы получить делимое, т.е. 12. Известно, что 4-3 = 12. Значит, 12:4 = 3.

Затем учащимся предлагается, рассуждая так же, найти, например, частное 8:4. И они сначала находят число, на которое надо умножить 4, чтобы получить 8. Получают число 2 и делают вывод - 8:4 = 2.

Далее, используя тот же способ рассуждений, находят частные 9:3,20:5 и др.

Видим, что умозаключения бывают разные. В примере 1 заключение логически следует из посылок, и мы не сомневаемся в его истинности. Такие умозаключения называют в логике дедуктивными.

О п р е д е л е н и е. Дедуктивным называется умозаключение, в котором посылки и заключение находятся в отношении логического следования.

Если посылки дедуктивного умозаключения обозначить буквами A₁, А₂, ... , А_n, а заключение - буквой В, то схематично само умозаключение можно представить так: A_1, А₂, ... А_n => В.

Часто используют такую запись: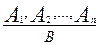

В ней черта заменяет слово «следовательно».

Дедуктивным является умозаключение, которое рассмотрено в примере 1.

Умозаключение, которое рассмотрено в примере 2, отлично от первого. В нем приведены три посылки частного характера, которые показывают, что некоторые натуральные числа обладают свойством: от перестановки множителей произведение не изменяется. И на этой основе сделан вывод, что этим , свойством обладают все натуральные числа. Такие умозаключения называют неполной индукцией.

О п р е д е л е н и е. Неполная индукция- это умозаключение, в котором на основании того, что некоторые объекты класса обладают определенным свойством, делается вывод о том, что этим свойством обладают все объекты данного класса.

Неполная индукция не является дедуктивным умозаключением, поскольку, рассуждая по такой схеме, можно прийти к ложному выводу.

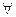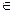Рассмотрим, например, такие выражения 3 + 5 и 3 · 5; 2 + 7 и 2 · 7; 4 + 8 и 4 · 8. Видим, что 3 + 5 < 3 · 5, 2 + 7 < 2 · 7,4 + 8 < 4 · 8, т.е. для некоторых натуральных чисел можно утверждать, что сумма меньше их произведения. И на основании того, что некоторые числа обладают указанным свойством, можно сделать вывод о том, что этим свойством обладают все натуральные числа, т.е. ( a, b N) a + b<a·b.

Но это утверждение ложно, в чем можно убедиться с помощью контрпримера: числа 1 и 2 - натуральные, но сумма 1 + 2 не меньше, чем произведение 1·2.

Вообще к выводам, полученным с помощью неполной индукции, надо относиться критически, так как они носят характер предположения, гипотезы и нуждаются в дальнейшей проверке: их надо либо доказать, либо опровергнуть.

Несмотря на то что неполная индукция не всегда приводит к истинным выводам, роль таких умозаключений в процессе познания велика. Почти все общие положения и, в частности, научные законы являются результатом умозаключений, называемых неполной индукцией.

Третий пример - это пример рассуждения по аналогии.

Слова «аналогия» в переводе с греческого означает «соответствие, сходство».

Вообще под аналогией понимают умозаключение, в котором на основании сходства двух объектов в некоторых признаках и при наличии дополнительного признака у одного из них делается вывод о наличии такого же признака у другого объекта.

Заметим, что в этом описании сути понятия «аналогия» термин «объект» используется в широком смысле: им может быть реальный предмет, модель, рисунок, числовое или буквенное выражение, задача и т.д. В качестве признаков могут выступать свойства объектов, отношения между ними, способы деятельности и т.д.

Аналогия помогает открывать новые знания, способы деятельности или использовать усвоенные способы деятельности в измененных условиях.

Вывод по аналогии носит характер предположения, гипотезы и поэтому нуждается либо в доказательстве, либо в опровержении.

Например, ученик установил, что число делится на 6, если оно делится на 2 и на 3. Затем, действуя по аналогии, сделал вывод: число делится на 8, если оно делится на 2 и на 4. Чтобы убедиться в ложности полученного вывода, достаточно привести контрпример: число 12 делится на 2 и на 4, но не делится на 8.

Широко используется аналогия в обучении математике младших школьников. Это происходит при изучении свойств объектов, отношений между ними и действий с ними. Приведем несколько примеров.

Аналогию можно использовать для «открытия» новых свойств изучаемых объектов. Например, если при изучении классов установлено, что в классе единиц три разряда - единицы, десятки, сотни, а в классе тысяч также три разряда -единица тысяч, десятки тысяч, сотни тысяч, то вывод о числе разрядов в классе миллионов и их названии дети могут сделать самостоятельно, по аналогии.

Аналогия может быть использована для установления отношений между данными объектами. Например, учащиеся установили, что 4· (3 + 7) > 4·3 + 4·6, так как 4· (3 + 7) = 4·3+4·7, а 4·7 > 4·6. Рассматривая затем выражения 3(8 + 9) и 3·8 + 3·7, учащиеся могут по аналогии сделать вывод о том, что 3 · (8 + 9) > 3 ·8 + 3·7. Проверить его правильность можно либо путем рассуждений, аналогичных тем, что проводились при выполнении первого задания либо при помощи вычислений.

Аналогия может быть использована и для выводов о способе действия на основе изучения другого способа. Так, после рассмотрения способа умножения двузначного числа на однозначное на примере умножения 27 на 3 (27·3 =

= (20+7) ·3 = 20·3+7·3 = 81) детям предлагается умножить 721 на 4. Действуя по аналогии, они устанавливают, что 712·4= (700+ 10 + 2) ·4 = 2800 + 40+8 = 2848. Далее по аналогии устанавливают, как умножить 6288 на 3.

Следующим шагом может быть обобщение, т.е. получение правила умножения многозначного числа на однозначное, т.е. использование неполной индукции.