Статистическое распределение выборки. Полигон. Гистограмма.

Генеральная совокупность и выборка

Пусть требуется изучить множество однородных объектов (это множество называется статистической совокупностью) относительно некоторого качественного или количественного признака, характеризующего эти объекты. Если сплошное обследование, т.е. изучение каждого объекта, невозможно, то из всей совокупности выбирают для изучения часть объектов. Статистическая совокупность, из которой отбирают часть объектов, называется генеральной совокупностью. Множество объектов, случайно отобранных из генеральной совокупности, называется выборкой.

Число объектов генеральной совокупности и выборки называется соответственно объёмом генеральной совокупности и объёмом выборки.

Пример. Плоды одного дерева (200 шт.) обследуют на наличие специфического для данного сорта вкуса. Для этого отбирают 10 шт. Здесь 200 – объём генеральной совокупности, 10 - объём выборки.

Если выборку отбирают по одному объекту, который обследуют и снова возвращают в генеральную совокупность, то выборка называется повторной. Если объекты выборки уже не возвращаются в генеральную совокупность, то выборка называется бесповторной. На практике чаще встречается бесповторная выборка.

Свойства объектов выборки должны правильно отражать свойства объектов генеральной совокупности, т.е. выборка должна быть репрезентативной (представительной). Считается, что выборка репрезентативна, если все объекты генеральной совокупности имеют одинаковую вероятность попасть в выборку, т.е. выбор производится случайно.

Статистическое распределение выборки. Полигон. Гистограмма.

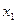Пусть из генеральной совокупности извлечена выборка, причём значение наблюдалось 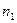раз, значение 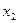- 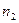раз, значение 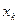- 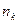раз и 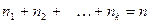– объём выборки. Наблюдаемые значения 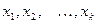называются вариантами, а последовательность вариант, записанная в возрастающем порядке, - вариационным рядом. Числа наблюдений 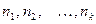называются частотами, а их отношения к объёму выборки 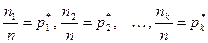– относительными частотами. Тогда .

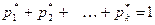Статистическим распределением выборки называется перечень вариант и соответствующих им частот (или относительных частот).

Статистическое распределение можно задать в виде последовательности интервалов и соответствующих им частот (непрерывное распределение). В качестве частоты, соответствующей интервалу, принимают сумму частот вариант, попавших в этот интервал. Для графического изображения статистического распределения используются полигоны и гистограммы.

Для построения полигона на оси OX откладывают значения вариант 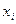, на оси OY – значения частот 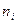(относительных частот ).

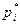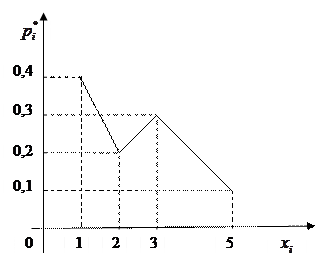
Пример. Постройте полигон для распределения:

Варианта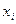
Относительная частота	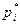0,4	0,2	0,3	0,1

В случае непрерывного распределения признака строят гистограммы. Интервал, в котором заключены все наблюдаемые значения признака, разбивают на несколько частичных интервалов длиной h и для каждого частичного интервала находят сумму частот вариант 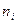, попавших в i–ый интервал. Затем на этих интервалах, как на основаниях, строят прямоугольники с высотам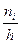и (или 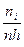, где n - объём выборки). Площадь i-го частичного прямоугольника равна 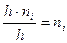(или 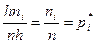). Следовательно, площадь гистограммы равна сумме всех частот, т.е. объёму выборки (или относительных частот, т.е. единице).

Пример. Изобразить гистограмму непрерывного распределения объёма n=100, приведённого в таблице.

Частичный интервал h	Сумма частот вариант частичного интервала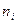
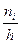
5-10 10-15 15-20 20-25 25-30 30-35 35-40		0,8 1,2 3,2 7,2 4,8 2,0 0,8