Уравнения Ома и Кирхгофа в матричной форме
Если в исследуемой сложной схеме содержатся параллельно включенные ветви, то для составления матриц соединений такие ветви необходимо заменить (объединить) одной эквивалентной ветвью.
В общем случае любая ветвь схемы кроме комплексного сопротивления (проводимости) 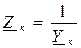 может содержать источник ЭДС Ек, источник тока Jк. Схема и граф обобщенной ветви показаны на рис. 1а, б:
может содержать источник ЭДС Ек, источник тока Jк. Схема и граф обобщенной ветви показаны на рис. 1а, б:

Ток ветви Iк, напряжение ветви Uк = j1 - j2.
Из потенциального уравнения ветви 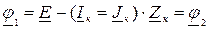 следуют:
следуют:
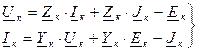 - уравнения Ома для к-ой ветви.
- уравнения Ома для к-ой ветви.
Для всех «m» ветвей составим систему уравнений по этой форме:
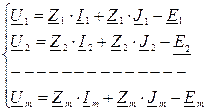
Заменим полученную систему из «m» уравнений матричной формой. Для этой цели введем следующие обозначения матриц:
|
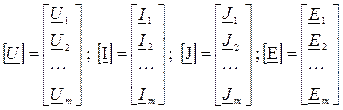

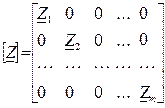 ;
; 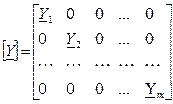
Уравнения Ома в матричной форме получат вид:
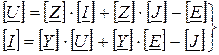
Уравнения Кирхгофа в обычной форме имеют вид: 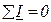 - первый закон Кирхгофа для узлов,
- первый закон Кирхгофа для узлов, 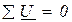 - второй закон Кирхгофа для контуров.
- второй закон Кирхгофа для контуров.
Система уравнений Кирхгофа в матричной форме получается через матрицы соединений 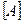 и
и 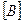 :
:
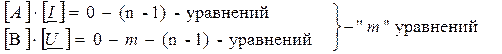
Составленная система уравнений содержит “m” неизвестных токов и “m” неизвестных напряжений, всего 2“m” неизвестных, и непосредственно не может быть решена.
|
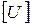 из матричных уравнений закона Ома, получим:
из матричных уравнений закона Ома, получим:
|
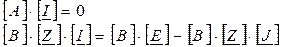
Для сравнения приведем те же уравнения в обычной форме:

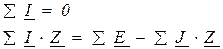
|
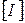 из матричного уравнения закона Ома, получим:
из матричного уравнения закона Ома, получим:
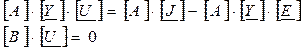
Для сравнения приведем те же уравнения в обычной форме:
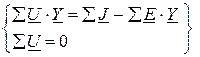
Дата добавления: 2016-10-18; просмотров: 2471;












