Проводимость плазмы

Рассмотрим простейший случай – проводимость в однородной плазме 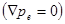для постоянного тока 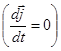. Уравнение (2.2.47) из предыдущего раздела принимает в этом случае вид:

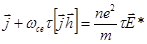(2.2.50)

где 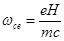- электронная циклотронная частота (2.2.51)

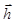- единичный вектор в направлении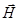

При 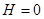или при 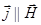из этого уравнения выпадает член с 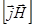и получается нормальная или продольная проводимость плазмы:

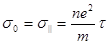(2.2.52)

Чтобы найти проводимость плазмы поперек магнитного поля, 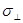, расписываем (2.2.50) в составляющих:

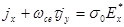(2.2.53)

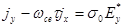(2.2.54)

Видно, что 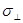есть величина тензорная. Удобнее выразить соотношения (2.2.52) - (2.2.54) с помощью тензора сопротивления 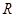, определяемого выражением:

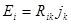(2.2.55)

Компоненты тензора образуют матрицу:

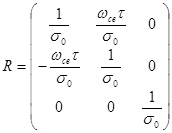(2.2.56)

Поскольку обычно вместо сопротивления 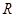пользуются тензором проводимости, который определяется равенством:

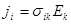, (2.2.57)

найдем его компоненты, Для этого нужно получить матрицу, обратную (2.2.56), то есть решить систему (2.2.53) - ( 2.2.54) относительно составляющих тока. В данном случае достаточно умножить одно из уравнений (2.2.53) - ( 2.2.54) на 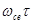и прибавить ко второму или вычесть из него, что даст в результате:

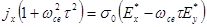(2.2.58)

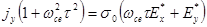(2.2.59)

Отсюда можно извлечь компоненты тензора проводимости однородной плазмы для постоянного тока:

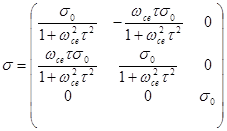(2.2.60)

В явном виде составляющие тока выражаются формулами:

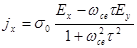(2.2.61)

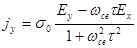(2.2.62)

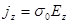, (2.2.63)

из которых видно, что условие замагниченности плазмы (то есть, в данном его понимании, существенности влияния магнитного поля на проводимость) выглядит следующим образом

.

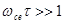2.3. Кинетический подход.

В случае использования гидродинамического подхода считается, что плазма представляет собой сплошную среду, выделенный элемент которой движется с некоторой скоростью. Скорости отдельных частиц не рассматриваются. Поскольку на самом деле в плазме происходит хаотическое движение множества частиц, имеющих различные скорости, то следует иметь в виду недостаточность гидродинамического подхода. Существует много явлений, которых этот подход не описывает. Дальнейшей детализацией описания процессов в плазме является статистический подход, реализуемый в рамках физической кинетики плазмы.

2.3.1. Фазовое пространство, функции распределения и их интегралы.

Введем основные понятия кинетического подхода к описанию плазмы. Исследование движения частиц в физической кинетике ведется в шестимерном фазовом пространстве.

Фазовое пространство– шестимерное конфигурационное пространство, координатами в котором служат три координаты обычного пространства: X,Y,Z и три соответствующие скорости :u_x,u_y,u_z, . Элемент объема такого пространства:

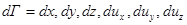(2.3.1)