Приближение бесконечной проводимости

Во многих случаях рассмотрение плазмы как проводящей жидкости может быть упрощено в еще большей степени: ее электрическое сопротивление устремляется к нулю. Это приближение называется приближением идеальной проводимости. В приближении идеальной проводимости электрическое поле в системе координат, связанной с плазмой, должно равняться нулю, ибо сколь угодно малое электрическое поле вызвало бы в идеальном проводнике бесконечно большой ток. Итак, полагаем 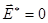, что может быть переписано следующим образом:

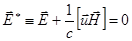(2.2.10)

или

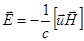(2.2.11)

Что фактически может быть заменено на

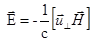(2.2.11а)

поскольку в векторное произведение дает вклад только перпендикулярная компонента скорости. Действительно, только пересечение проводником силовых линий магнитного поля проводит к возникновению в нем электродвижущей силы, дающей электрическое поле; движение его вдоль силовых линий никак не влияет на рассматриваемую ситуацию. Таким образом, условие (2.2.10) может быть трансформировано в требование, которому должно удовлетворять 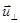- поперечная компонента скорости движущейся плазмы. 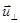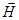Выразим используя (2.2.2а) для чего умножим обе части его на справа :

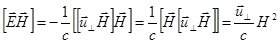(2.2.12)

Преобразование проведено с учетом того, что 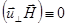и 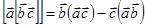. Из выражения (2.2.12) следует

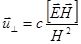или 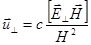(2.2.13)

Эти соотношения описывают дрейф в скрещенных электрическом и магнитном полях. Абсолютная величина скорости такого дрейфа

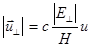(2.2.14)

Вмороженное поле

Идеальный проводник при своем движении не может пересекать силовых линий магнитного поля. Действительно, если бы такое пересечение имело бы место, возникшая ЭДС вызвала бы бесконечно большой ток, что в реальности невозможно. Следовательно, идеально проводящая плазма, будучи замагниченной, должна двигаться только вместе с силовыми линиями магнитного поля, не пересекая их. Вот как это выглядит в формальной записи. Выпишем одно из уравнений Максвелла, представляющее собой закон электромагнитной индукции:

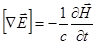(2.2.15)

С учетом соотношения, определяющего условие идеальной проводимости 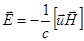, перепишем(2.2.15) в виде

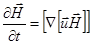(2.2.16)

или, раскрывая двойное векторное произведение:

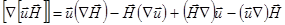(2.2.17)

с учетом равенства нулю дивергенции вектора напряженности магнитного поля, 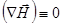, а также того, что

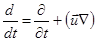(2.2.18),

получаем

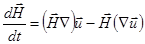(2.2.19)

Выпишем теперь уравнение непрерывности

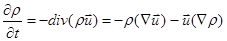(2.2.11)

Или, для однородной плазмы

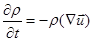(2.2.20)

Выразив отсюда 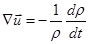, подставим в (2.2.16), после чего получим

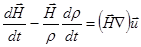(2.2.21)

Левую часть выражения (2.2.21) можно теперь выразить через производную по времени от величины 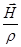. Заметим, что

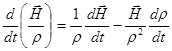(2.2.22)

откуда:

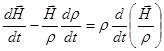(2.2.23)

поэтому (2.2.21) можно представить в виде:

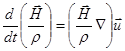(2.2.24)

Рассмотрим вначале простейший случай, когда скорость меняется только в направлении 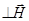. Тогда правая часть (2.2.24) обращается в нуль и, следовательно:

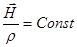(2.2.25)

При плоском сжатии вдоль поля:

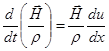
а уравнение непрерывности:

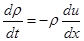
где 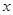- координата вдоль поля. Из сопоставления этих двух выражений следует:

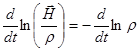
то есть 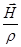меняется пропорционально 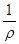, и следовательно:

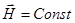
При сжатии вдоль поля 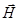не меняется.

Конечная проводимость, диффузия магнитного поля.

Если учесть конечную проводимость, то, используя закон Ома

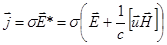(2.2.26)

можем записать:

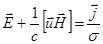(2.2.27)

Строго говоря 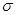- тензор, но в принятом приближении мы считаем его скаляром.

Выразив плотность тока из уравнений Максвелла 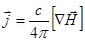- подставим в (2.2.27):

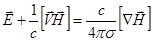(2.2.28)

Применив затем 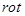к обеим частям (2.2.28)

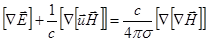(2.2.29)

и учитывая, что 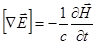, а также равенство нулю дивергенции магнитного поля 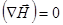и соотношение векторного анализа 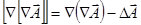, получаем окончательно

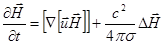(2.2.30)

Полученное уравнение отличается от уравнения с вмороженным полем наличием второго члена в правой части. Чтобы выяснить физический смысл этого слагаемого, рассмотрим простейший случай, когда движение вещества отсутствует 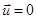тогда из (2.2.30) следует :

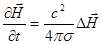
Полученное уравнение похоже на уравнение диффузии. Роль коэффициента диффузии играет величина:

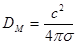, (2.2.31)

обратно пропорциональная проводимости плазмы. Можно сказать, что из-за конечной проводимости магнитное поле диффундирует сквозь плазму с коэффициентом диффузии, задаваемым формулой (2.2.31). Глубина его проникновения в течение заданного времени 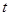оценивается как:

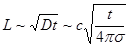(2.2.32)

Для периодического процесса характерное время измеряется периодом колебаний 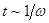и поэтому:

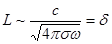- толщина скин-слоя

2.2.2. Двухжидкостная гидродинамика.

В одножидкостной модели, проводимость плазмы была введена нами просто, как произвольный параметр. Чтобы получить ее, исходя из физических реалий, нужно предложить модель, которая содержала бы в себе механизм проводимости - то есть нужно иметь более детальную модель. В качестве таковой может быть использована модель, в которой плазма рассматривается как совокупность двух “жидкостей”- электронной и ионной, движущихся одна сквозь другую. При этом электрическое сопротивление может быть представлено как результат взаимного трения двух этих жидкостей.

Запишем уравнения движения для двух жидкостей, считая, что на электроны действует только электронное давление 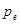, а на ионы – только ионное 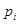. Взаимное трение – то есть передачу импульса при взаимодействии между частицами учтём введением сил трения 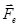и :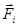

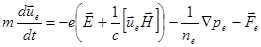(2.2.33)

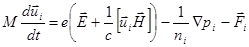(2.2.34)

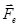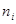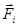пропорциональна и пропорциональна 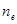. Представим 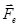и 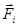как призведение коэффецента взаимного трения 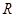на разность скоростей и на концентрацию тормозящих частиц:

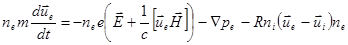(2.2.35)

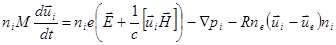(2.2.36)

Поскольку плазма квазинейтральна:

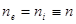(2.2.37)

плотность тока, выражаемая, как разность потока зарядов электронов и ионов:

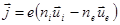(2.2.38)

может быть переписана в виде :

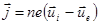(2.2.39)

Если сложить (2.2.35) и (2.2.36) с учётом (2.2.37) и (2.2.31) то силы электрического поля и трения взаимно уничтожатся. В результате получится уравнение МГД, в котором роль скорости течения плазмы 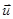играет средняя массовая скорость:

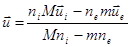(2.2.40)

так как 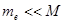, то:

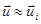(2.2.41)

В этом приближении из (2.2.39) получаем:

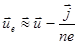(2.2.42)

Из законов механики следует, что передача импульса при взаимодействии пропорциональна приведённой массе 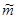взаимодействующих частиц. Удобно записать:

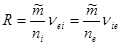(2.2.43)

Тогда система (2.2.35)- (2.2.36) принимает вид:

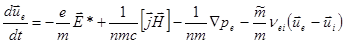(2.2.44)

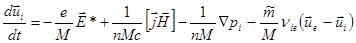(2.2.45)

здесь членом 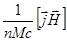можно пренебречь, а 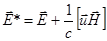- поле в сопутствующей системе координат, движущейся со среднемассовой скоростью. Из (2.2.43) видно что:

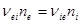
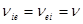(2.2.46)

Чтобы иметь полную систему макроскопических уравнений модели двух жидкостей, нужно получить уравнение для плотности тока – обобщённый закон Ома. В общем случае получение этого уравнения осложняется тем, что лагранжевы производные содержат нелинейные члены

.

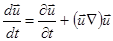Сравнительно просто получить закон Ома в случае, когда производные по времени вообще равны нулю (то есть для постоянного тока) и для колебаний малой амплитуды, когда можно пренебречь нелинейными членами и поменять 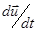на 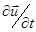(линейные колебания). Итак, если пренебречь членом вида 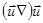, вычесть из второго (ионного) уравнения первое и отбросить члены, содержащие 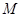в знаменателе (то есть пренебречь ускорением ионов) то, с учётом (2.2.39), получим:

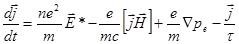(2.2.47)

где 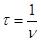(2.2.48)

При взаимодействии электронов и ионов приведенная масса:

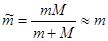(2.2.49)