Зависимость сопротивления металлов от температуры. Сверхпроводимость. Закон Видемана-Франца
Удельное сопротивление зависит не только от рода вещества, но и от его состояния, в частности, от температуры. Зависимость удельного сопротивления от температуры можно охарактеризовать, задавая температурный коэффициент сопротивления данного вещества:
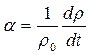 (14.11)
(14.11)
Он даёт относительное приращение сопротивления при увеличении температуры на один градус.
|
ρ=ρ0(1+αt) (14.12)
где ρ0 – удельное сопротивление при 0ºС, ρ – его значение при температуре tºС.
Температурный коэффициент сопротивления может быть как положительным, так и отрицательным. У всех металлов сопротивление увеличивается с увеличением температуры, а следовательно для металлов
α >0. У всех электролитов в отличии от металлов сопротивление при нагревании всегда уменьшается. Сопротивление графита с повышением температуры также уменьшается. Для таких веществ α <0.
 На основании электронной теории электропроводности металлов можно объяснить зависимость сопротивления проводника от температуры. С повышением температуры его удельное сопротивление увеличивается, а электропроводимость уменьшается. Анализируя выражение (14.7), видим, что электропроводимость пропорциональна концентрации электронов проводимости и средней длине свободного пробега <ℓ>, т.е. чем больше <ℓ>, тем меньшую помеху для упорядоченного движения электронов представляют соударения. Электропроводимость обратно пропорциональна средней тепловой скорости <υτ>. Тепловая скорость при повышении температуры возрастает пропорционально
На основании электронной теории электропроводности металлов можно объяснить зависимость сопротивления проводника от температуры. С повышением температуры его удельное сопротивление увеличивается, а электропроводимость уменьшается. Анализируя выражение (14.7), видим, что электропроводимость пропорциональна концентрации электронов проводимости и средней длине свободного пробега <ℓ>, т.е. чем больше <ℓ>, тем меньшую помеху для упорядоченного движения электронов представляют соударения. Электропроводимость обратно пропорциональна средней тепловой скорости <υτ>. Тепловая скорость при повышении температуры возрастает пропорционально 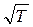 , что приводит к уменьшению электропроводимости и увеличению удельного сопротивления проводников. Анализируя формулу (14.7), можно, кроме того, объяснить зависимость γ и ρ от рода проводника.
, что приводит к уменьшению электропроводимости и увеличению удельного сопротивления проводников. Анализируя формулу (14.7), можно, кроме того, объяснить зависимость γ и ρ от рода проводника.
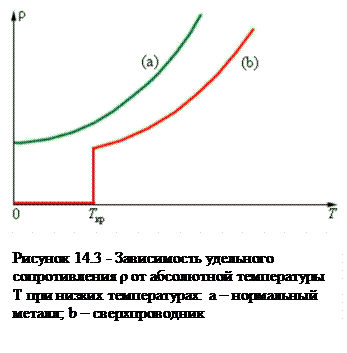
При очень низких температурах порядка 1-8ºК сопротивление некоторых веществ резко падает в миллиарды раз и практически становится равным нулю.
Это явление, впервые открыто голландским физиком Г.Камерлинг-Оннесом в 1911 г.. называется сверхпроводимостью. В настоящее время сверхпроводимость установлена у целого ряда чистых элементов (свинца, олова, цинка, ртути, алюминия и др), а также у большого числа сплавов этих элементов друг с другом и с другими элементами. На рис. 14.3 схематически показана зависимость сопротивления сверхпроводников от температуры.
Теория сверхпроводимости была создана в 1958 г. Н.Н. Боголюбовым. Согласно этой теории, сверхпроводимость – это движение электронов в кристаллической решётке без соударений друг с другом и с атомами решётки. Все электроны проводимости движутся как один поток невязкой идеальной жидкости, не взаимодействуя между собой и с решёткой, т.е. не испытывая трения. Поэтому сопротивление сверхпроводников равно нулю. Сильное магнитное поле, проникая в сверхпроводник, отклоняет электроны, и, нарушая «ламинарное течение» электронного потока, вызывает соударение электронов с решёткой, т.е. возникает сопротивление.
В сверхпроводящем состоянии между электронами происходит обмен квантами энергии, что приводит к созданию между электронами сил притяжения, которые больше кулоновских сил отталкивания. При этом образуются пары электронов (куперовские пары) с взаимно скомпенсированными магнитными и механическими моментами. Такие пары электронов движутся в кристаллической решётке без сопротивления.
Одним из важнейших практических применений сверхпроводимости является применение её в электромагнитах со сверхпроводящей обмоткой. Если бы не существовало критического магнитного поля, разрушающего сверхпроводимость, то с помощью таких электромагнитов можно было бы получать магнитные поля в десятки и сотни миллионов ампер на сантиметр. Получать такие большие постоянные поля с помощью обычных электромагнитов невозможно, так как для этого потребовались бы колоссальные мощности, и был бы практически невозможен отвод тепла, выделяемого при поглощении обмоткой столь больших мощностей. В сверхпроводящем электромагните расход мощности источника тока ничтожен, а расход мощности на охлаждение обмотки до гелиевой температуре (4,2ºК) на четыре порядка ниже, чем в обычном электромагните, создающем такие же поля. Сверхпроводимость применяется и для создания систем памяти электронных математических машин (криотронные элементы памяти).
В 1853 г. Видеман и Франц опытным путём установили, что отношение теплопроводности λ к электропроводности γ для всех метал лов при одной и той же температуре одинаково и пропорционально их термодинамической температуре.
Это заставляет предполагать, что теплопроводность в металлах, так же как и электропроводность, обусловлена движением свободных электронов. Будем считать, что электроны подобны одноатомному газу, коэффициент теплопроводности которого, согласно кинетической теории газов, равен
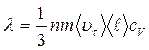 (14.13)
(14.13)
(n – концентрация атомов, m -масса атома, <ℓ> -средняя длина свободного пробега электрона, cV-удельная теплоёмкость).
Для одноатомного газа
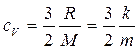
(k -постоянная Больцмана, М –молярная масса).
Тогда
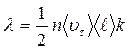 (14.14)
(14.14)
Из уравнений (14.7) и (14.14) находим отношение теплопроводности и электропроводности металла:
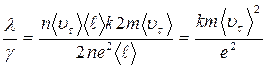 (14.15)
(14.15)
Из кинетической теории газов известно, что 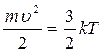 , тогда
, тогда
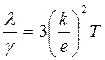 (14.16)
(14.16)
( k и е – постоянные величины).
Поэтому отношение теплопроводности и электропроводности металла пропорционально термодинамической температуре, что и было установлено законом Видемана-Франца. Так как k =1,38∙10-23Дж/К; е = 1,6∙10-19Кл, то
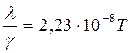 (14.17)
(14.17)
Закон Видемана-Франца для большинства металлов выполняется при температуре 100-400 К, но при низкой температуре закон существенно нарушается. Имеются металлы (бериллий, марганец) которые совсем не подчиняются закону Видемана-Франца. Выход из непреодолимых противоречий был найден в квантовой электронной теории металлов.
Дата добавления: 2016-07-27; просмотров: 7194;











