Показатели изменения уровней ряда динамики

Одним из важнейших направлений анализа рядов динамики является изучение особенностей развития явления за отдельные периоды времени.

С этой целью для динамических рядов рассчитывают ряд показателей:

1. К – темпы роста.

2. 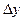– абсолютные приросты.

3. 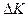– темпы прироста.

Темп роста – относительный показатель, получающийся в результате деления двух уровней одного ряда друг на друга. Темпы роста могут рассчитываться как цепные, когда каждый уровень ряда сопоставляется с предшествующим ему уровнем: 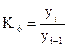, либо как базисные, когда все уровни ряда сопоставляются с одним и тем же уровнем 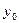, выбранным за базу сравнения: 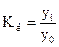. Темпы роста могут быть представлены в виде коэффициентов либо в виде процентов.

Абсолютный прирост – разность между двумя уровнями ряда динамики, имеет ту же размерность, что и уровни самого ряда динамики. Абсолютные приросты могут быть цепными и базисными, в зависимости от способа выбора базы для сравнения:

– цепной абсолютный прирост - ;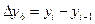

– базисный абсолютный прирост - .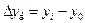

Для относительной оценки абсолютных приростов рассчитываются показатели темпов прироста.

Темп прироста – относительный показатель, показывающий на сколько процентов один уровень ряда динамики больше (или меньше) другого, принимаемого за базу для сравнения.

Базисные темпы прироста: .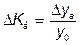

Цепные темпы прироста: .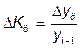

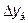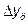где и – абсолютный базисный или цепной прирост;

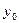– уровень ряда динамики, выбранный за базу для определения базисных абсолютных приростов;

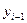– уровень ряда динамики, выбранный за базу для определения i-го цепного абсолютного прироста.

Существует связь между темпами роста и прироста:

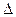К = К – 1 или 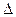К = К – 100% (если темпы роста определены в процентах).

Если разделить абсолютный прирост (цепной) на темп прироста (цепной) за соответствующий период, получим показатель, называемый – абсолютное значение одного процента прироста: .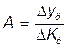

7.4. Определение среднего абсолютного прироста,
средних темпов роста и прироста

По показателям изменения уровней ряда динамики (абсолютные приросты, темпы роста и прироста), полученным в результате анализа исходного ряда, могут быть рассчитаны обобщающие показатели в виде средних величин – средний абсолютный прирост, средний темп роста, средний темп прироста.

Средний абсолютный прирост может быть получен по одной из формул:

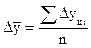или ,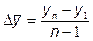

где n – число уровней ряда динамики;

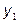– первый уровень ряда динамики;

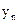– последний уровень ряда динамики;

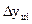– цепные абсолютные приросты.

Средний темп роста можно определить, пользуясь формулами:

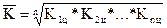
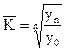
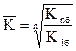
где n – число рассчитанных цепных или базисных темпов роста;

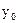– уровень ряда, принятый за базу для сравнения;

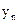– последний уровень ряда;

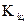– цепные темпы роста (в коэффициентах);

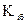– первый базисный темп роста;

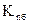– последний базисный темп роста.

Между темпами прироста 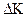и темпами роста К существует соотношение 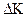= К – 1, аналогичное соотношение верно и для средних величин.