Этапы компьютерного моделирования

Для компьютерного моделирования можно выделить три ступени развития. Первая ступень связана с началом появления точных наук. Поэтому некоторые методы вычислений носят имена таких корифеев наук, как Ньютон, Эйлер, а слово «алгоритм» происходит от имени средневекового арабского ученого Аль - Хорезми. Вторая ступень начинается с 50-х годов 20 века, когда появились скромные по нынешним меркам ЭВМ (компьютеры), которые избавили ученых от огромной по объему вычислительной работы. Сейчас общество подошло к третьей ступени развития, когда моделирование «встраивается» в структуры информационного общества.

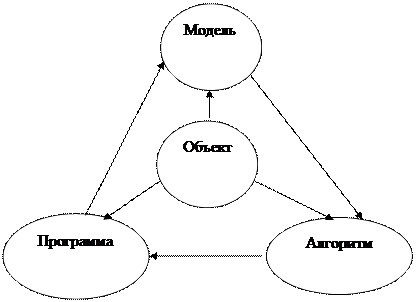Компьютерное моделирование какого-либо объекта порождает такой план действий, который можно разбить на три этапа: модель – алгоритм – программа (рис. 1.2).

Рисунок 1.2 - Технология компьютерного моделирования

На первом этапе строится «эквивалент» объекта. Этот «эквивалент» отражает в математической форме важные для данного исследования свойства объекта: законы, которым подчиняется объект, связи, присущие его частям и т.д. Затем математическая модель исследуется теоретическими методами, что позволяет получить предварительные знания об объекте.

Второй этап – разработка алгоритма для реализации модели на компьютере. Модель представляется в форме, удобной для применения численных методов, определяется последовательность вычислительных и логических операций, которые нужно произвести, чтобы найти искомые величины с заданной точностью. Вычислительные алгоритмы не должны искажать основные свойства модели и, следовательно, исходного объекта, быть экономичными и адаптирующимися к особенностям решаемых задач и используемых компьютеров.

На третьем этапе создаются программы, «переводящие» модель и алгоритм на доступный компьютеру язык. К ним также предъявляются требования экономичности и адаптивности. Их можно назвать «электронным» эквивалентом изучаемого объекта, уже пригодным для испытания на компьютере.

Создав триаду «модель – алгоритм – программа», исследователь получает в руки универсальный, гибкий и недорогой инструмент, который отлаживается и тестируется в «пробных» вычислительных экспериментах. После того, как адекватность (достаточное соответствие) триады исходному объекту имеется, с моделью проводятся разные «опыты», дающие все требуемые свойства и характеристики объекта. Важно, что процесс моделирования сопровождается улучшением и уточнением всех звеньев триады.

Такой метод познания сочетает в себе преимущества и теории, и эксперимента. Действительно, работа не с самим объектом (явлением или процессом), а с компьютерной моделью дает возможность относительно быстро, без существенных затрат исследовать его свойства и поведение в любых мыслимых ситуациях. Это составляет преимущества теории. В то же время вычислительные эксперименты с моделями объектов позволяют, опираясь на мощь вычислительных методов и компьютеров, глубоко и полно изучать объекты, что недоступно чисто теоретическим подходам. Это уже составляет преимущества эксперимента.

Компьютерное моделирование как методология не подменяет собой математику, физику, биологию и другие научные дисциплины, а играет синтезирующую роль. Создание и применение триады невозможно без опоры на самые разные методы и подходы - от качественного анализа нелинейных моделей до современных языков программирования.

Но, решая проблемы информационного общества, нельзя уповать только на мощь компьютеров. Необходимо постоянное совершенствование триады математического моделирования.