Критические напряжения и способы их определения

Л. Эйлер при выводе своей формулы определения опасной силы для сжимаемых стержней (10.2) предполагал, что материал стержня достаточно упруг и следует закону Гука.

Как известно, материал следует закону Гука только до тех пор, пока напряжения в нем не достигнут предела пропорциональности. Следовательно, формула Эйлера для разных материалов должна иметь свои пределы применимости. Она справедлива только до тех пор, пока эйлеровы напряжения в стержне не превзойдут предела пропорциональности материала: .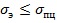

Анализ формулы (10.6) показывает, что эйлеровы напряжения зависят от геометрических размеров стержня, выражаемых его гибкостью 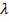. Так, для коротких стержней эйлеровы напряжения (10.6) оказываются выше придела пропорциональности. Поэтому для таких стержней формула Эйлера не применима.

Область применимости формулы (10.6) найдем, приравняв :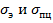

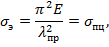
где 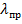– предельное значение гибкости стержня, показывающее границы применимости формулы Эйлера с точки зрения геометрических размеров стержня, откуда

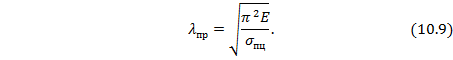
Поэтому формула Эйлера (10.6) справедлива при

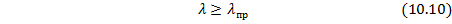
На основании определенных механических характеристик материалов по пределу пропорциональности найдем их предельные значения гибкости: для стали 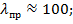для чугуна 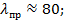для дерева (сосна) 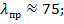для дюралюминия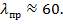

При меньшей гибкости чем при 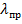потеря устойчивости стержня происходит в области пластических деформаций, где не применим закон Гука и формулы Эйлера (10.5) и (10.6). В этом случае используются приближенные подходы по определению опасного напряжения при сжатии стержня в пластической стадии, т.е. критического напряжения .

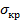Критические напряжения в судостроительных расчетах определяются по графику акад. Ю.А. Шиманского (рис. 10.6): вычислив эйлеровы напряжения 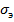по фомуле (10.6) и зная предел текучести материала 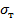, из графика находят:

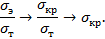
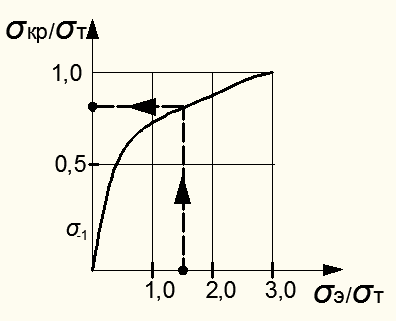
Рисунок 10.6 – График акад. Ю.А. Шиманского по определению критических напряжений

В машиностроительных расчетах критические напряжения вычисляют по эмпирической формуле проф. Ф.С. Ясинского:

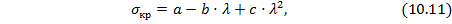
где a, b, c – опытные коэффициенты, зависящие от материала и имеющие размерность напряжения; 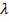– гибкость стержня.

Для стального и дюралюминиевого стержней формула Ясинского применима при гибкостях

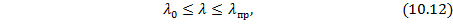
где 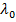– значение гибкости, при котором критическое напряжение равно пределу текучести материала стержня; при гибкости, меньшей 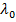, критическое напряжение принимается постоянным и равным пределу текучести.

Определенные значения опытных коэффициентов для различных материалов следующие:

· для стали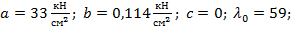

· для дюралюминия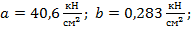

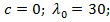
· для чугуна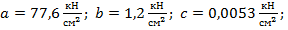

· для дерева (сосна, ель)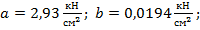

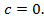
Соотношение эйлеровых и критических напряжений:

а) в упругой области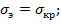

б) в области пластических деформаций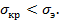

Критическая сила вычисляется по формуле:

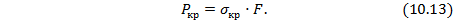
Допускаемые напряжения при продольном изгибе 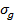до предела пропорциональности и за пределом пропорциональности зависит от материала и гибкости стержня, т.е. от величины λ, причем его можно рассматривать как некоторую часть 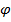от допускаемого напряжения на простое сжатие 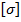. Тогда

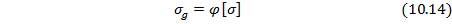
Коэффициент 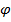всегда меньше единицы. Он называется коэффициентом уменьшения допускаемых напряжений для сжатых стержней. Коэффициент 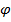зависит от гибкости стержня λ и материала. Таким образом, вводя коэффициент 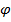, проверку на продольный изгиб можно производить как и в случае простого сжатия, но с уменьшением допускаемых напряжений на сжатие.

Значение коэффициента 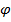в зависимости от гибкости стержня λ и вида основных конструкционных материалов приводятся в таблице:

Таблица 10.1 – Значения коэффициентов 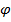при продольном изгибе стержня

Гибкость λ	Материал
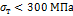
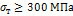
Сталь,	Сталь	Чугун	Дерево
	1,00	1,00	1,00	1,00
	0,99	0,98	0,97	0,99
	0,97	0,95	0,91	0,97
	0,95	0,92	0,81	0,93
	0,92	0,89	0,69	0,87
	0,89	0,84	0,57	0,80
	0,86	0,78	0,44	0,71
	0,81	0,71	0,34	0,60
	0,75	0,63	0,26	0,48
	0,69	0,54	0,20	0,38
	0,60	0,46	0,16	0,31
	0,52	0,39	-	0,25
	0,45	0,33	-	0,22
	0,40	0,29	-	0,18
	0,36	0,25	-	0,16
	0,32	0,23	-	0,14
	0,29	0,21	-	0,12
	0,26	0,19	-	0,11
	0,23	0,17	-	0,10
	0,21	0,15	-	0,09
	0,19	0,13	-	0,08

Расчеты на продольный изгиб разделяют на два типа: определение допускаемы нагрузок и подбор сечений стержней.