Определение динамических напряжений и перемещений при ударе

Рассмотрим какую-либо неподвижную защемленную упругую систему, на которую с высоты h падает груз весом Р (рис.11,а-г). пройдя путь h, груз, движущийся с некоторой скоростью, приходит в соприкосновение с неподвижной системой. Это явление называется ударом. При изучении такого явления в сопротивлении материалов используется приближенная теория удара, которая основывается на следующих допущениях:

а) удар является неупругим, т.е. груз после соприкосновения с конструкцией движется совместно с нею;

б) напряжения в стержне при ударе не превышают предела пропорциональности, а потому при изучении удара можно использовать закон Гука;

в) деформации распространяются в стержне мгновенно.

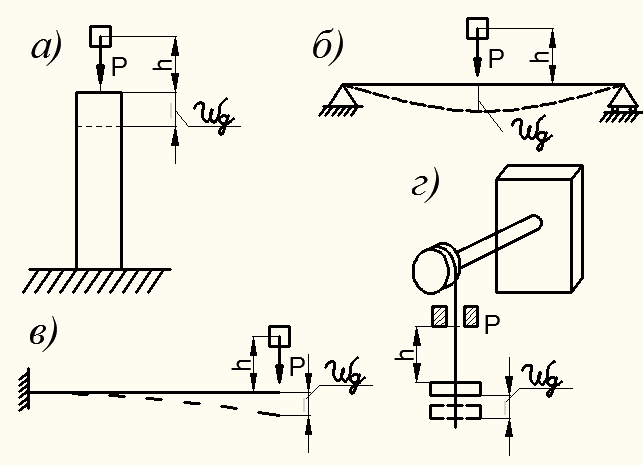
Рисунок 11.1 – Примеры систем подвергающихся удару

Система, подвергающаяся удару, может испытывать различные виды деформаций: сжатие (рис. 11.1, а); изгиб (рис. 11.1, б, в); кручение с изгибом (рис. 11.1, г).

Целью расчета этих систем на удар является определение наибольших напряжений и перемещений, возникающих в результате удара.

Приближенная теория удара предполагает определение динамических напряжений 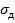и перемещений 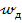вследствие удара через статические напряжения 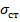и перемещения 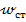от статически приложенной силы Р через коэффициент динамичности 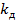по формулам:

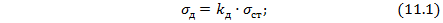
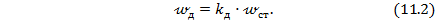
Как видно из формул (11.1) и (11.2), коэффициент динамичности показывает, во сколько раз динамические напряжения или перемещения больше статических ( ).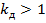

Коэффициент динамичности при ударе без учета собственной массы конструкции, подвергающейся удару, рассчитывается по формуле:

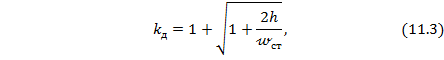
где h – высота падения ударяющего груза.

В частном случае при мгновенном безударном приложении силы, т.е. при 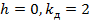. Следовательно, при внезапном ударном действии как напряжения, так и перемещения получаются вдвое больше, чем при статическом действии нагрузки.