Исследование функции на экстремумы

Исследование функций с помощью производной, построение графиков

Определение промежутков возрастания и убывания функций

Функция 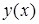называется возрастающей, если для любого 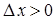выполняется условие 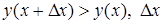– приращение независимой переменной или аргумента.

Другими словами, большим значениям переменной соответствуют большие значения функции. Из определения возрастающей функции следует, что ее приращение 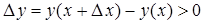, следовательно, для возрастающей функции

.

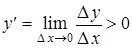Функция 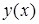называется убывающей, если для любого 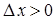выполняется условие .

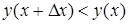Другими словами, большим значениям переменной соответствуют меньшие значения функции. Из определения убывающей функции следует, что ее приращение 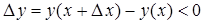, следовательно, для убывающей функции

.

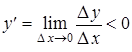Исследование функции на экстремумы

Значение 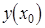называется максимумом функции 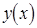, если существует окрестность точки 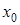такая, что для всех точек из этой окрестности выполняется неравенство , .

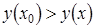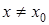Другими словами, значение функции в точке максимума больше всех соседних значений функции.

Значение 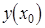называется минимумом функции 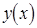, если существует окрестность точки 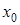такая, что для всех точек из этой окрестности выполняется неравенство , .

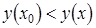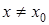Другими словами, значение функции в точке минимума меньше всех соседних значений функции.

Максимум и минимум функции называются также одним словом – экстремум функции.

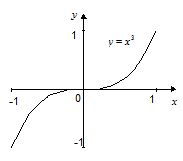
Экстремумы могут быть “гладкими”, как на рисунках внизу.

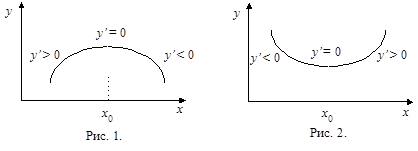
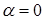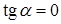Касательные, проведенные к графику функции в точках экстремума, параллельны оси OX. Пусть a – угол между касательной и положительным направлением оси OX, тогда и , а так как 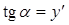, то производная 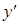в точках “гладкого” экстремума равна 0. Точки, в которых производная равна 0, называются стационарными. Однако не в каждой стационарной точке имеется экстремум функции. На рисунке представлен график функции 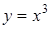, ее производная при 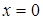равна 0, но из рисунка видно, что никакого экстремума при 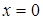у функции нет. Из рисунков 1 и 2 видно, что вблизи экстремума производная функции должна менять знак: вблизи максимума с “+” на “–”, а вблизи минимума с “–”на “+”.

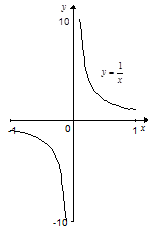
Экстремумы функции могут быть “острыми”, как на рисунках 3 и 4. Касательные к графику функции, проведенные при 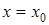, образуют прямой угол с OX ( 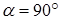), следовательно, значение 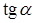в точках острого экстремума не существует (не определено), а т.к. 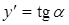, то не существует и производная. Как и в предыдущем случае, можно заметить, что не для всех значений переменной, для которых производная не существует, будет существовать экстремум функции.

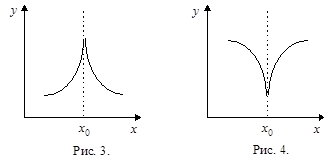
Рассмотрим график функции 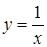; её производная 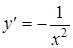при 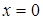не существует, но и сама функция в этой точке не определена, поэтому определение экстремума для этой точки не применимо (нет значения, которое можно сравнивать с другими).

Итак, чтобы исследовать функцию на экстремум, нужно найти производную. Затем найти критические точки: те значения переменной, при которых производная равна 0 или не существует. Из критических точек выбрать те, где сама функция непрерывна (определена). Для таких точек проверить смену знака производной вблизи критических точек: если производная меняет знак с “+” на “–”, значит, в данной точке максимум, при смене знака с “–”на “+” в точке имеется минимум; если смены знака не происходит, экстремума нет.