Определение промежутков выпуклости и вогнутости

Функция называется выпуклой (выпуклой вверх) на данном промежутке, если ее график лежит не выше касательной, проведенной в любой точке этого промежутка (рис. 5).

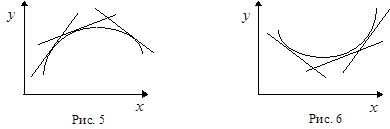
Функция называется вогнутой (выпуклой вниз) на данном промежутке, если ее график лежит не ниже касательной, проведенной в любой точке этого промежутка (рис. 6).

Примечание: наличие касательной предполагает, что функция является дифференцируемой на промежутке.

На рис. 5 видно, что на участке выпуклости функция вначале возрастает, затем убывает, т.е. первая производная меняет знак с “+” на “–”, другими словами, убывает. Следовательно вторая производная 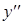(производная от 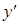) отрицательна (см. п. 6.1.). Аналогично, из рис. 6 видно, что на участке вогнутости функция вначале убывает, затем возрастает, т.е. первая производная меняет знак с “–”на “+”, возрастает и, следовательно, 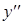(производная от 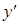) положительна.

Чтобы определить промежутки выпуклости и вогнутости функции, нужно найти ее вторую производную 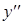, определить критические точки второй производной, т.е. точки, в которых она равна нулю или не существует. Затем определить знак второй производной в промежутках между критическими точками, например, методом интервалов.