Определение наименьшего и наибольшего значения функции на промежутке

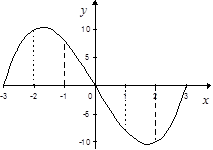
Рассмотрим для примера график функции 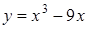. На промежутке 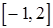наибольшее значение функции достигается на левом конце промежутка при 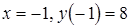; наименьшее – в точке минимума при .

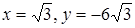Если взять промежуток 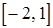, то наибольшее значение достигается в точке максимума при 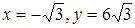, а наименьшее – на правом конце промежутка при 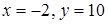. На промежутке 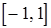наибольшее значение функции на левом конце при 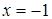, наименьшее – на правом при .

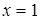Следовательно, в зависимости от выбранного промежутка изменения переменной x наибольшее или наименьшее значение непрерывной функции может достигаться или на концах промежутка, или в точках экстремума.

При наличии точек разрыва первого рода наибольшее или наименьшее значение функции может совпадать с одним из односторонних пределов функции.

Если же на выбранном промежутке функция имеет точку (точки) разрыва второго рода, то в данном случае дело обстоит следующим образом:

а) если справа и слева от точки разрыва функция стремится к +¥, то наибольшее значение функции на промежутке определить нельзя;

б) если справа и слева от точки разрыва функция стремится к –¥, то наименьшее значение функции определить нельзя;

в) если с одной стороны точки разрыва функция стремится к +¥, а с другой – к –¥, то нельзя определить ни наименьшее, ни наибольшее значение функции.

Итак, чтобы найти наибольшее или наименьшее значение непрерывной функции на промежутке, нужно найти производную функции и определить ее критические точки. Затем вычислить значения функции на концах промежутка и в тех критических точках, которые попадают на промежуток. Из полученных значений выбрать наибольшее и наименьшее значение.