Приемы корреляционного анализа
Приемы корреляционного анализа используются для измерения влияния факторов в стохастическом анализе, когда взаимосвязь между показателями неполная, вероятностная.

|
Различают парную и множественную корреляцию.
Парная корреляция — это связь между двумя показателями, один из которых является факторным, а другой — результативным. Множественная корреляция возникает от взаимодействия нескольких факторов с результативным показателем.
Необходимые условия применения корреляционного анализа:
а) наличие достаточно большого количества наблюдений о величине исследуемых факторных и результативных показателей (в динамике или за текущий год по совокупности однородных объектов);
б) исследуемые факторы должны иметь количественное измерение и отражение в тех или иных источниках информации.
Применение корреляционного анализа позволяет:
во-первых, определить изменение результативного показателя пoд воздействием одного или нескольких факторов (в абсолютном изме- рении), т.е. узнать, на сколько единиц изменяется величина резуль- тативного показателя при изменении факторного на единицу;
во-вторых, установить относительную степень зависимости ре- зультативного показателя от каждого фактора.
Первая задача решается путем подбора и обоснования соответству- ющего типа уравнения связи и нахождения его параметров. В зависи- мости от характера связи различают прямолинейную и криволиней-ную зависимость, которая обосновывается с помощью графиков аналитических группировок и т.д.
Зависимость результативного показателя от определяющих его
факторов можно выразить уравнением парной и множественной рег-

|
рессии. При прямолинейной форме они имеют следующий вид:
§ уравнение прямой регрессии: уХ=а+bx
Для иллюстрации корреляционного анализа прямолинейной за- висимости используем приведенные в табл. 3.4 данные об изменения
уровня выработки рабочих (у) в зависимости от уровня фондовооруженности труда (х).
Расчет уравнения связи (ух= а + bх) сводится к определению параметров а и b. Их находят из следующей системы уравнений:
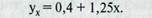
|
Уравнение связи, описывающее зависимость производительноcти труда от фондовооруженности, получило следующее выражение:
Коэффициент а — постоянная величина результативного показателя, которая не связана с изменением данного фактора. Параметр b показывает среднее изменение результативного показателя с повышением или понижением величины фактора на единицу его измерения. В данном примере с увеличением фондовооруженности труда на 1 тыс. руб. выработка рабочих повышается в среднем на 1,25 тыс. руб.
Подставляя в уравнение регрессии соответствующие значения х, можно определить выравненные (теоретические) значения результативного показателя (ух) для каждого предприятия. Например, чтобы рассчитать выработку рабочих на первом предприятии, где фондовооруженность труда равна 3,1 тыс. руб., необходимо сделать следующий расчет:
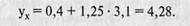
Полученная величина показывает, какой была бы выработка при фондовооруженности труда 3,1 тыс. руб., если бы данное предприятие использовало свои производственные мощности в такой степени, каш в среднем все предприятия данной выборки. Фактическая выработка на данном предприятии выше расчетного значения. Следовательно, данное предприятие использует свои производственные мощности несколько лучше, чем в среднем по отрасли. Аналогичные расчеты сделаны для каждого предприятия. Данные приведены в последней графе 1 табл. 4.3. Сравнение фактического уровня выработки рабочих с расчетным позволяет оценить результаты работы отдельных предприятий.»
По такому же принципу решается уравнение связи при криволинейной зависимости между изучаемыми явлениями. Когда при увеличении одного показателя значения другого возрастают до определенного уровня, а потом начинают снижаться (например, зависимость производительности труда рабочих от их возраста), то для описания такой зависимости лучше всего подходит парабола второго порядка:
Кроме параболы для описания криволинейной зависимости в корреляционном анализе очень часто используется гипербола:
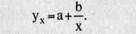
|
Для определения ее параметров необходимо решить следующую систему уравнений:
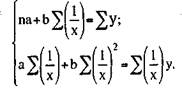
Гипербола описывает такую зависимость между двумя показателями, когда при увеличении одной переменной значения другой увеличиваются до определенного уровня, а потом прирост замедляется: зависимость урожайности от количества внесенного удобрения, продуктивности животных – от уровня их кормления, себестоимости единицы продукции – от объема ее производства и др.
При более сложном характере зависимости между изучаемыми явлениями используются более сложные параболы (третьего, четвертого порядка и т.д.), а также квадратические, степенные, показательные и другие функции.
Таким образом, используя тот или иной тип математического уравнения, можно определить степень зависимости между изучаемыми явлениями, узнать, на сколько единиц в абсолютном измерении изменяется величина результативного показателя с изменением факторного на единицу. Однако регрессионный анализ не дает ответа на вопрос, тесная эта связь или нет, решающее или второстепенное воздействие оказывает данный фактор на величину результативного показателя.
Для измерения тесноты связи между факторными и результативными показателями исчисляется коэффициент корреляции. В случае прямолинейной формы связи между изучаемыми показателями он рассчитывается по следующей формуле:
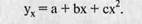
В соответствии с требованиями метода наименьших квадратов для 8 определения параметров a, b и с необходимо решить следующую систему уравнений:
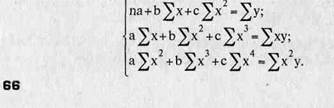
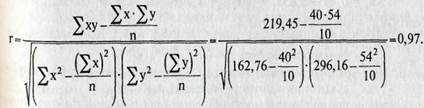
Коэффициент корреляции может принимать значения от 0 до 1. Чем ближе его величина к 1, тем более тесная связь между изучаемы-
ми явлениями, и наоборот. В данном случае величина коэффициента) корреляции является существенной (r = 0,97). Это позволяет сделать вывод о том, что фондовооруженность — один из основных факторов, от которых на анализируемых предприятиях зависит уровень производительности труда.
Если коэффициент корреляции возвести в квадрат, получим ко- эффициент детерминации (d = 0,94). Он показывает, что производи- тельность труда на 94% зависит от фондовооруженности труда, а на долю других факторов приходится 6% изменения ее уровня.
Для измерения тесноты связи при криволинейной форме зависимости используется не линейный коэффициент корреляции, а корреляционное отношение, формула которого имеет следующий вид:
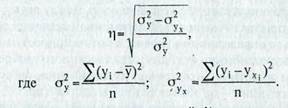
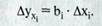
|
Эта формула является универсальной. Ее можно применять для исчисления коэффициента корреляции при любой форме зависимости. Однако для его нахождения требуются предварительное решение уравнения регрессии и расчет по нему теоретических (выравненных) значений результативного показателя для каждого наблюдения исследуемой выборки (см. гр. 7 табл. 4.3).
Решение задач многофакторного корреляционного анализа производится на ПЭВМ по типовым программам. Сначала формируется матрица исходных данных, в первой графе которой записывается порядковый номер наблюдения, во второй - величина результативного показателя (у), а в следующих — данные по факторным показателям (х1). Эти сведения вводятся в ПЭВМ и затем рассчитывается уравнение множественной регрессии, которое в нашей задаче получило следующее выражение:

Коэффициенты уравнения показывают количественное воздействие каждого фактора на результативный показатель при неизменности других. В данном случае можно дать следующую интерпретацию полученному уравнению: рентабельность повышается на 3,65% при увеличении материалоотдачи на 1 руб.; на 0,09% - с ростом фондоотдачи на 1 коп.; на 1,02% — с повышением среднегодовой выработки продукции на одного работника на 1 тыс. руб.; на 0,052% - при увеличении удельного веса продукции высшей категории качества на 1%. С увеличением продолжительности оборота средств на 1 день рентабельность снижается в среднем на 0,122%.
Коэффициент множественной корреляции равен 0,92, коэффициент множественной детерминации — 0,85. Это значит, что изменение уровня рентабельности на 85% зависит от исследуемых факторов, а на долю других факторов приходится 15% вариации результативного показателя. Значит, данное уравнение можно использовать для практических целей:
а) расчета влияния факторов на прирост результативного показа
теля;
б) подсчета резервов повышения уровня исследуемого показателя;
в) планирования и прогнозирования его величины.
Влияние каждого фактора на изменение величины результативного показателя рассчитывается следующим образом:
Допустим, что уровень материалоотдачи на анализируемом предприятии по плану на отчетный год - 2,5 руб., а фактически - 2,4 руб. Из-за этого уровень рентабельности продукции ниже планового на 0,365%
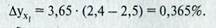
|
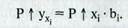
|
Аналогичным образом подсчитывают резервы роста результативного показателя. Для этого планируемый прирост факторного показателя умножают на соответствующий ему коэффициент регрессии в Уравнении связи:
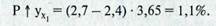
|
Предположим, что в следующем году намечается рост материалоотдачи с 2,4 до 2,7 руб. За счет этого рентабельность повысится на
Подобные расчеты делаются по каждому фактору с последующим обобщением результатов анализа.
Результаты многофакторного регрессионного анализа могут быть также использованы для планирования и прогнозирования уровня результативного показателя. С этой целью необходимо в полученное урав-
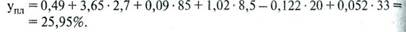
|
| нение связи подставить плановый (прогнозный) уровень факторных показателей: |
Таким образом, многофакторный корреляционный анализ имеет важную научную и практическую значимость. Это проявляется в том, что значительно углубляется факторный анализ, устанавливаются место и роль каждого фактора в формировании уровня исследуемых показателей и, как результат, точнее обосновываются планы и управленческие решения, объективнее оцениваются итоги деятельности предприятий и полнее определяются внутрихозяйственные резервы.
Вопросы и задания
1. Назовите основные приемы, используемые для измерения влия- ния факторов в детерминированном факторном анализе.
2. Охарактеризуйте сущность, область применения и процедуру рас- четов приемами цепной подстановки, абсолютных разниц, отно- сительных разниц, пропорционального деления, интегральным методом, методом логарифмирования.
3. Для чего и в каких случаях используются приемы корреляцион-ного анализа? Каковы его задачи?
4. Как решается уравнение связи при прямолинейной и криволи- нейной зависимости? Как интерпретируются его коэффициенты?
5. Для чего и как рассчитывается коэффициент корреляции при пря- молинейной и криволинейной зависимости? Что показывает ве- личина коэффициентов корреляции и детерминации?
6. Как проводится многофакторный корреляционный анализ?
7. Для каких целей и каким образом используются результаты кор- реляционного анализа?
8. На основании приведенных данных запишите факторную модель фонда заработной платы и рассчитайте влияние факторов на из- менение ее суммы всеми возможными способами:
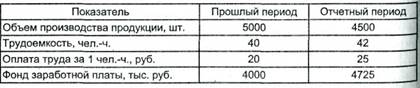
9. На основании приведенных данных составьте факторную модель прибыли и рассчитайте влияние факторов на изменение ее суммы всеми возможными способами:
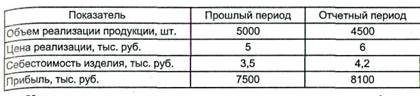
10. На основании приведенных данных определите уровень фондоотдачи и рассчитайте влияние факторов на изменение ее уровня всеми возможными способами:

11. На основании приведенных данных рассчитайте влияние факторов на изменение продолжительности оборота капитала способом пропорционального деления:
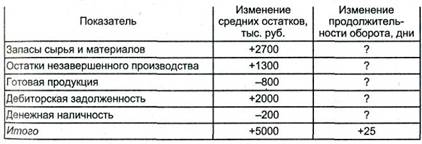
12. На основании приведенных данных о затратах (х) и объемах производства продукции (у) рассчитайте уравнение связи и коэффициенты корреляции и детерминации и дайте им экономическую интерпретацию:

13. Уравнение связи, описывающее зависимость уровня фондоотдачи от степени изношенности основных средств, получило следующее выражение:
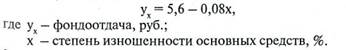
Дайте экономическую интерпретацию этого уравнения и определите резерв роста фондоотдачи, если степень изношенности основных средств снизится с 40 до 35%.
Глава 5
Дата добавления: 2016-10-18; просмотров: 4900;











