Траектория материальной точки, путь, перемещение
Траекторией материальной точки называется линия, описываемая этой точкой в пространстве при ее движении. В зависимости от формы траектории различают прямолинейное и криволинейное движения точки. Если все участки траектории точки лежат в одной плоскости, то движение точки называют плоским. Уравнения (1.2.3) и (1.2.4) задают траекторию точки в так называемой параметрической форме. Роль параметра играет время 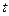 . Решая эти уравнения совместно и, исключая из них время
. Решая эти уравнения совместно и, исключая из них время 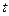 , находят уравнение траектории.
, находят уравнение траектории.
|
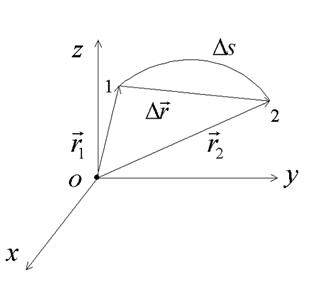
| Рис 1.3.1 |
Длина траектории, описаннойматериальной точкой за некоторый промежуток времени 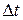 называется путем
называется путем 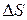 , пройденным точкой за это время.
, пройденным точкой за это время.
Вектор, проведенный из начального положения (точка 1) в конечное положение (точка 2) называется перемещением 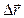 .
.
Из рис. 1.3.1 видно, что вектор перемещения равен приращению радиус-вектора точки за промежуток времени 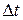 .
.
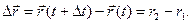
| (1.3.1) |
Так как 
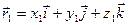 , ,
| (1.3.2) |
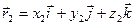 , ,
| (1.3.3) |
то
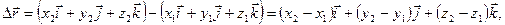
| (1.3.4) |
или
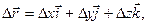
| (1.3.4) |
где 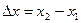 ;
; 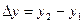 ;
; 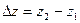 .
.
При прямолинейном движении вектор перемещения совпадает с соответствующим участком траектории. В общем случае 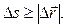
Скорость
Для описания движения материальной точки вводят векторную физическую величину – скорость, определяющую как быстроту движения, так и направление движения в данный момент времени.
|
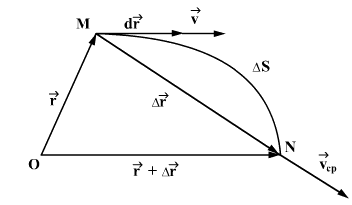
| Рис 1.4.1 |
Пусть материальная точка движется по криволинейной траектории 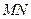 так, что в момент времени
так, что в момент времени 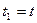 она находится в точке
она находится в точке 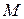 , а в момент времени
, а в момент времени 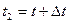 в точке
в точке 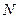 . Радиус-векторы точек
. Радиус-векторы точек 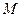 и
и 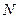 соответственно равны
соответственно равны 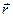 и
и 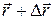 , а длина дуги
, а длина дуги 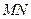 равна пройденному пути
равна пройденному пути 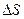 (рис. 1.4.1).
(рис. 1.4.1).
Вектором средней скорости 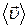 точки в интервале времени от
точки в интервале времени от 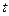 до
до 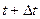 называют отношение вектора перемещения
называют отношение вектора перемещения 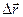 к промежутку времени
к промежутку времени 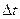 , за который это перемещение произошло:
, за который это перемещение произошло:
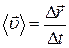 . .
| (1.4.1) |
Вектор средней скорости направлен в сторону вектора перемещения 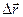 , т.е. вдоль хорды
, т.е. вдоль хорды 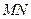 .
.
Модуль вектора средней скорости
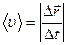 . .
| (1.4.2) |
Предел отношения 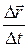 при
при 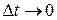 представляет собой вектор скорости
представляет собой вектор скорости 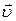 материальной точки в данный момент времени
материальной точки в данный момент времени 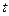 , то есть в момент прохождения ее через точку
, то есть в момент прохождения ее через точку 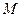 траектории.
траектории.
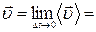 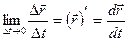 . .
| (1.4.3) |
Она называется мгновенной скоростью.
Вектор мгновенной скорости равен первой производной от радиус-вектора по времени.
В процессе уменьшения величины 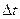 точка
точка 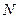 приближается к точке
приближается к точке 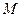 , и хорда
, и хорда 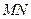 , поворачиваясь вокруг точки
, поворачиваясь вокруг точки 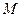 , в пределе совпадает по направлению с касательной к траектории в точке
, в пределе совпадает по направлению с касательной к траектории в точке 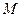 . Поэтому векторы
. Поэтому векторы 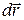 и
и 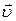 движущейся точки направлены по касательной к траектории в сторону движения.
движущейся точки направлены по касательной к траектории в сторону движения.
Модуль вектора мгновенной скорости равен первой производной от пути по времени.
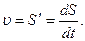
|
Вектор мгновенной скорости 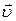 материальной точки можно разложить на три составляющих вектора, направленных вдоль осей прямоугольной декартовой системы координат.
материальной точки можно разложить на три составляющих вектора, направленных вдоль осей прямоугольной декартовой системы координат.
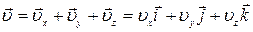 , ,
| (1.4.4) |
где 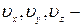 проекции вектора скорости на оси координат
проекции вектора скорости на оси координат 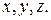
Подставляя в (1.4.3) значения для радиус-вектора материальной точки (1.2.1) и выполнив почленное дифференцирование, получим:
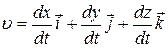 . .
| (1.4.5) |
Из сопоставления выражений (1.4.4) и (1.4.5) следует, что проекции вектора мгновенной скорости материальной точки на оси прямоугольной декартовой системы координат равны первым производным по времени от соответствующих координат точки:
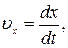 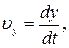 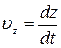 . .
| (1.4.6) |
Поэтому модуль мгновенной скорости:
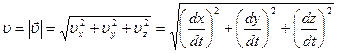
| (1.4.7) |
В системе СИ единица измерения скорости называется метр в секунду 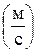 .
.
Движение, при котором направление вектора скорости материальной точки не изменяется, называется прямолинейным.
Если численное значение (модуль) мгновенной скорости точки остается во время движения неизменным, то такое движение называется равномерным.
Если же за произвольные равные промежутки времени точка проходит разные расстояния, то модуль ее мгновенной скорости с течением времени изменяется. Такое движение называют неравномерным.
Ускорение
Ускорение характеризует быстроту изменения вектора мгновенной скорости.
Вектор среднего ускорения равен отношению вектора изменения скорости 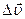 к промежутку времени
к промежутку времени 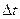 , в течение которого это изменение произошло
, в течение которого это изменение произошло
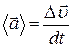 . .
| (1.5.1) |
Направление вектора среднего ускорения совпадает с направлением вектора 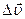 .
.
Модуль вектора среднего ускорения
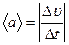 . .
| (1.5.2) |
Вектор мгновенного ускорения равен пределу вектора среднего ускорения при стремлении промежутка времени 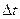 к нулю
к нулю
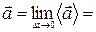 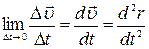 . .
| (1.5.3) |
В проекциях на соответствующие координаты оси:
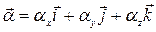 ,
,
или
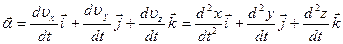 . .
| (1.5.4) |
В системе СИ единица измерения ускорения называется метр в секунду за секунду 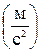 .
.
Дата добавления: 2016-10-07; просмотров: 4794;











