Тело отсчета. Система отсчета. Радиус-вектор материальной точки. Кинематические уравнения движения материальной точки
Понятие механики. Модели в механике
Механика – часть физики, которая изучает закономерности механического движения и причины, вызывающие или изменяющие это движение.
Механическим движением называется изменение с течением времени взаимного расположения тел или их частей.
Механика состоит из трех частей: кинематика, динамика и статика. Кинематика (от греч. kinema – движение) занимается математическим
описанием различных видов движения тел без учета их массы и действующих на них сил.
Динамика (от греч. dynamis – сила) изучает движение тел с учетом действующих на них сил.
Статика (от греч. statike – равновесие) изучает условия равновесия тел. Поскольку равновесие есть частный случай движения, законы статики являются естественным следствием законов динамики.
В классической механике Галилея и Ньютона рассматривается движение макроскопических тел со скоростями, значительно меньшими, чем скорость света в вакууме. Движение тел со скоростями, близкими к скорости света, изучает релятивистская механика, основанная на специальной теории относительности. Рассмотрением движения элементарных частиц занимается квантовая механика.
Для описания механического движения тел в зависимости от условия задачи используют различные физические модели. Чаще других используют понятия абсолютно твердого тела и материальной точки.
Движение тел происходит под действием сил. Под действием внешних сил тела могут деформироваться, т.е. изменять свои размеры и форму.
Тело, деформацией которого можно пренебречь в условиях данной задачи, называют абсолютно твердым телом.
Тело, размерами и формой которого в данной задаче можно пренебречь, называется материальной точкой.
Тело отсчета. Система отсчета. Радиус-вектор материальной точки. Кинематические уравнения движения материальной точки
Всякое движение относительно, поэтому для описания движения необходимо условиться, относительно какого другого тела будет отсчитываться перемещение данного тела. Выбранное для этой цели тело называют телом отсчета.
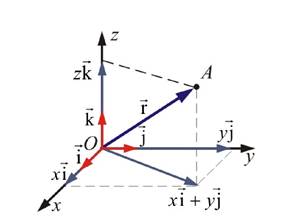
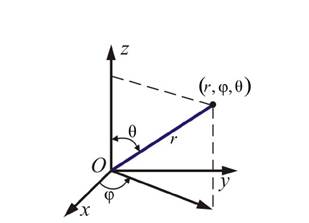
Для описания движения практически приходится связывать с телом отсчета систему координат (декартову (рис. 1.2.1), сферическую (рис. 1.2.2), цилиндрическую и др.).
| 
|
| Рис. 1.2.1 | Рис. 1.2.2 |
Пространство трехмерно, поэтому «естественной» системой координат является, декартова, или прямоугольная система координат, которой мы в основном и будем пользоваться при изучении поступательного движения тел.
Движение тела происходит не только в пространстве, но и во времени, поэтому при изучении движения используют прибор для измерения времени.
Совокупность системы координат, тела отсчета, с которым она связана и прибора для измерения времени называют системой отсчета.
В декартовой системе координат положение точки 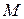 в данный момент времени по отношению к этой системе можно задать с помощью трех скалярных координат
в данный момент времени по отношению к этой системе можно задать с помощью трех скалярных координат 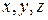 , или с помощью радиус-вектора
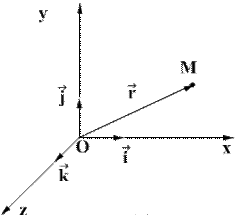
, или с помощью радиус-вектора 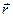 , проведенного из начала координат в эту точку (рис. 1.2.3).
, проведенного из начала координат в эту точку (рис. 1.2.3).
|
| Рис 1.2.3 |
Его проекции на координатные оси равны декартовым координатам данной точки: 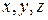 . Умножив их на единичные векторы (орты) осей
. Умножив их на единичные векторы (орты) осей 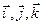 , вектор
, вектор 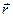 можно представить в виде
можно представить в виде
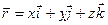
| (1.2.1) |
Слагаемые 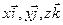 называются компонентами, или составляющими, вектора
называются компонентами, или составляющими, вектора 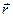 ; числа
; числа 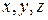 – координатами конца вектора, а само соотношение (1.2.1) – формулой разложения вектора
– координатами конца вектора, а само соотношение (1.2.1) – формулой разложения вектора 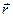 по единичным ортам.
по единичным ортам.
Модуль радиус-вектора 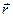 , используя теорему Пифагора, можно выразить по формуле
, используя теорему Пифагора, можно выразить по формуле
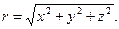
| (1.2.2) |
При движении материальной точки 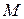 ее координаты
ее координаты 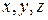 и радиус-вектор
и радиус-вектор  изменяются с течением времени
изменяются с течением времени 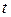 . Поэтому для задания закона движения материальной точки необходимо указать либо вид функциональной зависимости всех трех ее координат от времени:
. Поэтому для задания закона движения материальной точки необходимо указать либо вид функциональной зависимости всех трех ее координат от времени:
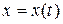 , , 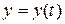 , , 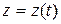 , ,
| (1.2.3) |
либо зависимость радиус-вектора точки от времени
 . .
| (1.2.4) |
Три скалярных уравнения (1.2.3) или эквивалентное им одно векторное уравнение (1.2.4.) называются кинематическими уравнениями движения материальной точки.
Число независимых координат, полностью определяющих положение точки в пространстве, называется числом степеней свободы.
Если материальная точка движется в пространстве, то она имеет три степени свободы (координаты 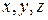 ); если точка движется на плоскости – две степени свободы; если вдоль линии – одну степень свободы.
); если точка движется на плоскости – две степени свободы; если вдоль линии – одну степень свободы.
Дата добавления: 2016-10-07; просмотров: 2634;











