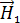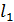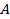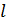Магнитное поле в веществе
План решения задач
1.При расчете магнитного поля катушки с ферромагнитным сердечником следует иметь в виду, что индукция магнитного поля 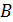 в таком сердечникезависит от напряженности МП
в таком сердечникезависит от напряженности МП 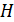 .Причем, вид зависимости
.Причем, вид зависимости 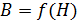 для конкретного материала сердечника устанавливается экспериментально. Как правило, в справочной литературе и в задачниках по физике приводят графики зависимостей
для конкретного материала сердечника устанавливается экспериментально. Как правило, в справочной литературе и в задачниках по физике приводят графики зависимостей 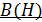 .
.
2. Чтобы воспользоваться такой зависимостью, вычисляют напряженность магнитного поля 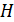 , обычно, с помощью теоремы о циркуляции вектора
, обычно, с помощью теоремы о циркуляции вектора 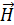 . В правой части теоремы записывают сумму токов, охватываемых контуром интегрирования
. В правой части теоремы записывают сумму токов, охватываемых контуром интегрирования 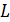 (вдоль которого определяется циркуляция), как число ампер-витков катушки
(вдоль которого определяется циркуляция), как число ампер-витков катушки 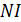 . Это произведение числа витков
. Это произведение числа витков 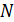 в обмотке катушки на силу тока
в обмотке катушки на силу тока 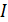 .
.
3. Магнитную проницаемость 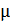 материала сердечника вычисляют по формуле связи величин
материала сердечника вычисляют по формуле связи величин  :
:  . Отметим, что величина магнитной проницаемости
. Отметим, что величина магнитной проницаемости 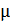 зависит не только от напряженности намагничивающего поля, но и от размеров и формы ферромагнитного сердечника. Для бесконечного (тороидального или кольцевого) сердечника величина
зависит не только от напряженности намагничивающего поля, но и от размеров и формы ферромагнитного сердечника. Для бесконечного (тороидального или кольцевого) сердечника величина 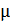 наибольшая и достигает значений
наибольшая и достигает значений  . Поперечная прорезь в сердечнике приводит к существенному снижению его магнитной проницаемости.
. Поперечная прорезь в сердечнике приводит к существенному снижению его магнитной проницаемости.
Задача 55.Магнитный момент атома железа 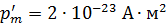 . Оцените магнитный момент
. Оцените магнитный момент  железного бруска длиной
железного бруска длиной 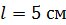 и площадью сечения
и площадью сечения  , намагниченного до насыщения. Определите максимальный вращающий момент
, намагниченного до насыщения. Определите максимальный вращающий момент 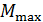 , который действовал бы на такой железный брусок в магнитном поле с индукцией
, который действовал бы на такой железный брусок в магнитном поле с индукцией  .
.
Дано Решение
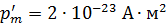 ; ;
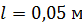 ; ;
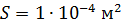 ; ;
 ; ;
 ; ;

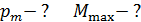
|
Железный брусок, как и другие ферромагнетики, состоит из доменов. Домен – это область самопроизвольной намагниченности вещества, причем, в пределах домена векторы магнитных моментов всех атомов сонаправлены, т. е. каждый домен намагничен до насыщения. Размер домена порядка (0,01…0,1) мм, число атомов вещества в таком домене  . В размагниченном состоянии ферромагнетика магнитные моменты его доменов
. В размагниченном состоянии ферромагнетика магнитные моменты его доменов 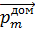 имеют хаотическую ориентацию. Но во внешнем магнитном поле с индукцией
имеют хаотическую ориентацию. Но во внешнем магнитном поле с индукцией 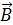 на каждый домен, имеющий магнитный момент
на каждый домен, имеющий магнитный момент 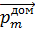 , действует механический (вращающий) момент
, действует механический (вращающий) момент  , модуль которого
, модуль которого 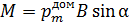 . В результате поворота магнитных моментов доменов сначала растут домены, у которых угол
. В результате поворота магнитных моментов доменов сначала растут домены, у которых угол 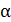 между векторами
между векторами 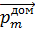
 мал. На заключительной стадии намагничивания ферромагнетика происходит поворот магнитных моментов выросших доменов до состояния с
мал. На заключительной стадии намагничивания ферромагнетика происходит поворот магнитных моментов выросших доменов до состояния с 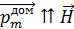 , где
, где 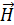 – напряженность намагничивающего поля. При этом образец представляет собой один домен, магнитный момент которого
– напряженность намагничивающего поля. При этом образец представляет собой один домен, магнитный момент которого
 , (1)
, (1)
где 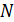 – число атомов в бруске;
– число атомов в бруске;  – магнитный момент атома железа.
– магнитный момент атома железа.
Таким образом, в бруске ферромагнетика, намагниченном до насыщения, магнитные моменты всех атомов сонаправлены. В результате этого, согласно равенству (1), модуль магнитного момента железного бруска определяется следующей формулой:
 (2)
(2)
Число атомов  в бруске определим, используя число Авогадро
в бруске определим, используя число Авогадро  , равное числу атомов в одном моле вещества, умножая это число на количество вещества (число молей)
, равное числу атомов в одном моле вещества, умножая это число на количество вещества (число молей) 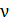 :
:
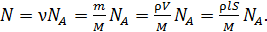 (3)
(3)
Здесь 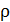 – плотность железа;
– плотность железа; 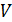 – объем бруска, имеющего размеры
– объем бруска, имеющего размеры  ;
; 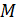 – молярная масса железа.
– молярная масса железа.
Подставляя число атомов 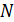 по формуле (3) в равенство (2), получаем расчетную формулу магнитного момента бруска в виде:
по формуле (3) в равенство (2), получаем расчетную формулу магнитного момента бруска в виде:
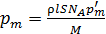 .
.
Вычислим магнитный момент данного железного бруска, намагниченного до насыщения:
 .
.
Полученная величина магнитного момента бруска является достаточно большой. Такой магнитный момент имел бы виток:  , например, при токе
, например, при токе 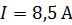 и площади витка
и площади витка  . Другой объект, имеющий магнитный момент, – соленоид; для него величина
. Другой объект, имеющий магнитный момент, – соленоид; для него величина 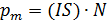 , где
, где 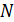 – число витков. Вычислим магнитный момент соленоида, имеющего ту же площадь сечения, как и брусок:
– число витков. Вычислим магнитный момент соленоида, имеющего ту же площадь сечения, как и брусок:  . Этот оценочный расчет показывает, что катушка с воздушным сердечником имеет такой же магнитный момент, как и железный брусок, при числе витков катушки
. Этот оценочный расчет показывает, что катушка с воздушным сердечником имеет такой же магнитный момент, как и железный брусок, при числе витков катушки  .
.
Механический момент 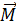 , действующий в магнитном поле с индукцией
, действующий в магнитном поле с индукцией 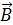 на объект, обладающий магнитным моментом
на объект, обладающий магнитным моментом 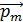 , определяется следующей формулой:
, определяется следующей формулой:
 модуль
модуль 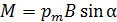 , (4)
, (4)
где 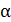 – угол между векторами
– угол между векторами 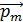 и
и 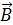 .
.
Максимальная величина механического момента 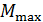 , согласно формуле (4), наблюдается при значении
, согласно формуле (4), наблюдается при значении 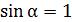 , т. е. при расположении вектора магнитного момента бруска
, т. е. при расположении вектора магнитного момента бруска  . Вычисляем эту величину по формуле (4):
. Вычисляем эту величину по формуле (4):
 .
.
Для того чтобы удержать такой намагниченный железный брусок в положении, при котором его магнитный момент  , необходимо к концам бруска приложить пару сил, каждая из которых
, необходимо к концам бруска приложить пару сил, каждая из которых  . Это сила тяжести
. Это сила тяжести 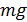 груза массой 17 кг. Такой оценочный расчет показывает, как велики магнитные силы, действующие на ферромагнитные объекты.
груза массой 17 кг. Такой оценочный расчет показывает, как велики магнитные силы, действующие на ферромагнитные объекты.
Задача 56. Железное кольцо средним радиусом  и площадью поперечного сечения
и площадью поперечного сечения  является сердечником кольцевого соленоида. Его обмотка содержит
является сердечником кольцевого соленоида. Его обмотка содержит  с током
с током  . Определите магнитную индукцию
. Определите магнитную индукцию 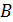 поля в сердечнике, магнитный поток
поля в сердечнике, магнитный поток 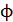 в сечении кольца и магнитную проницаемость сердечника
в сечении кольца и магнитную проницаемость сердечника 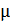 . Используйте график основной кривой намагничивания железа:
. Используйте график основной кривой намагничивания железа: 

|
Железное кольцо:
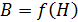 ; ;
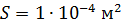 ; ;

|

Рис. 86 |
|

Рис. 87 |
Так как магнитная индукция 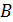 железного сердечника зависит от напряженности
железного сердечника зависит от напряженности 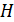 магнитного поля в нем (рис. 86), рассчитаем величину
магнитного поля в нем (рис. 86), рассчитаем величину 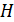 при заданном токе. Для этого запишем теорему о циркуляции вектора
при заданном токе. Для этого запишем теорему о циркуляции вектора 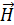 вдоль контура интегрирования
вдоль контура интегрирования 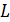 , совпадающего со средней линией кольца, длина которой
, совпадающего со средней линией кольца, длина которой 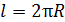 . Направление обхода по контуру
. Направление обхода по контуру 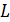 (рис. 87) выбираем так, чтобы проекция
(рис. 87) выбираем так, чтобы проекция  вектора
вектора 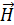 на направление элемента длины контура
на направление элемента длины контура 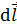 была положительной. В таком случае
была положительной. В таком случае
 (1)
(1)
Из этого уравнения определяем напряженность МП и вычисляем ее:
 .
. 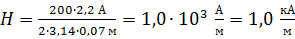 .
.
По графику  (см. рис. 86) для найденной величины
(см. рис. 86) для найденной величины  определяем
определяем  .
.
Магнитный поток в сечении сердечника определяем с учетом того, что линии магнитной индукции (сонаправленные линиям напряженности МП) являются окружностями, концентрическими кольцу. Такие линии поля перпендикулярны сечению сердечника площадью 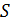 (см. рис. 87), поэтому проекция вектора
(см. рис. 87), поэтому проекция вектора 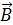 на нормаль к сечению
на нормаль к сечению 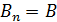 . Магнитное поле в тонком кольце практически однородно и магнитный поток
. Магнитное поле в тонком кольце практически однородно и магнитный поток  .
.
Вычисляем магнитный поток в сечении железного сердечника:
 .
.
Величина магнитной проницаемости железного сердечника
 .
.
Вычисляем по этой формуле магнитную проницаемость железа при найденной напряженности МП и соответствующем ей значении 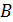 :
:
 .
.
Это значение не является максимальным для железа. С помощью графика  можно оценить наибольшее значение магнитной проницаемости
можно оценить наибольшее значение магнитной проницаемости 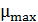 по наибольшему угловому коэффициенту
по наибольшему угловому коэффициенту  прямой
прямой  :
:
 . По графику находим величину
. По графику находим величину  . Соответствующее значение
. Соответствующее значение 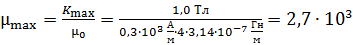 .
.
Задача 57. Тороидальная катушка с железным сердечником, длина осевой линии которого 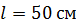 , имеет обмотку, содержащую
, имеет обмотку, содержащую 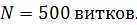 При токе в обмотке тороида
При токе в обмотке тороида 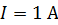 индукция магнитного поля в сердечнике
индукция магнитного поля в сердечнике  Какой ток
Какой ток 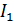 нужно пропустить по обмотке для получения магнитного поля с такой же величиной
нужно пропустить по обмотке для получения магнитного поля с такой же величиной 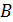 в воздушном зазоре сердечника? Длина воздушного промежутка
в воздушном зазоре сердечника? Длина воздушного промежутка  (рис. 88), рассеянием магнитного потока в зазоре можно пренебречь.
(рис. 88), рассеянием магнитного потока в зазоре можно пренебречь.
Дано Решение
 ; ;
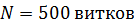 ; ;
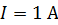 ; ;
 ; ;
 . .

|
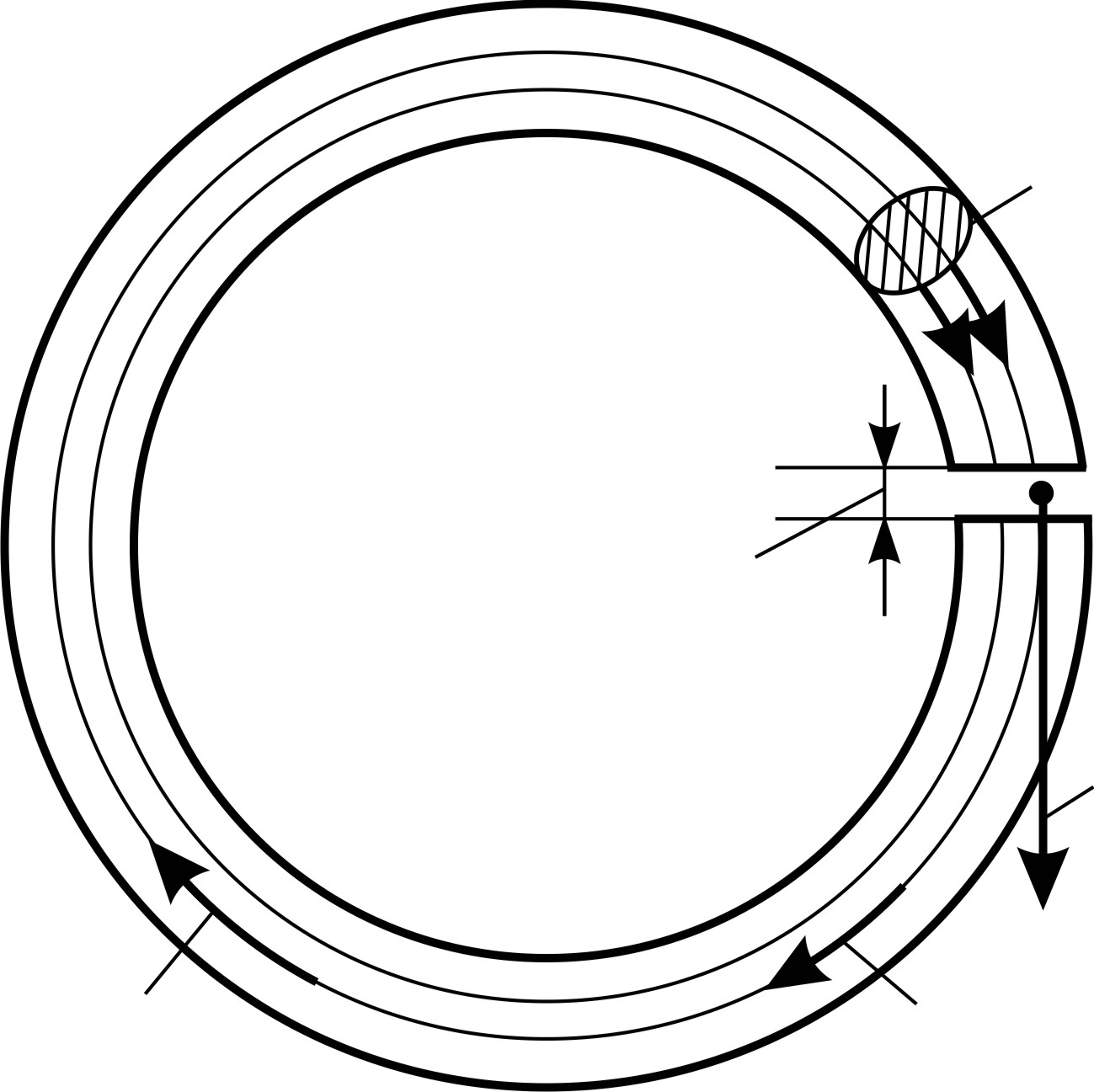
Рис. 88 |
Если пренебречь рассеянием магнитного потока в зазоре, т. е. принять, что магнитный поток в сердечнике 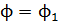 – магнитному потоку в воздушном промежутке, то
– магнитному потоку в воздушном промежутке, то
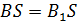 ;
; 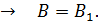
Таким образом, магнитная индукция поля в сердечнике и в воздушном промежутке одинакова. Но напряженности МП различны:
а) в сердечнике с магнитной проницаемостью 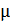 величина
величина  ; (1)
; (1)
б) в воздушном промежутке (для воздуха 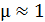 ) –
) – 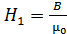 . (2)
. (2)
Величина магнитной индукции 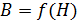 ; эта зависимость для железа задана графиком (см. рис. 86). Для получения той же величины
; эта зависимость для железа задана графиком (см. рис. 86). Для получения той же величины  в случае сердечника с зазором напряженность магнитного поля
в случае сердечника с зазором напряженность магнитного поля 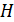 внутри сердечника должна быть такой же, как и в сплошном сердечнике (это одна и та же точка на графике
внутри сердечника должна быть такой же, как и в сплошном сердечнике (это одна и та же точка на графике 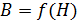 ).
).
С учетом этих замечаний запишем теорему о циркуляции вектора 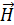 вдоль контура интегрирования
вдоль контура интегрирования 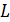 , совпадающего с осевой линией сердечника. Искомый ток
, совпадающего с осевой линией сердечника. Искомый ток 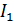 содержится в правой части теоремы:
содержится в правой части теоремы:
а) для сплошного сердечника –
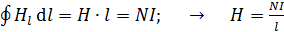 ; (3)
; (3)
б) в случае сердечника с воздушным промежутком (см. рис. 88) –
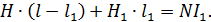 (4)
(4)
Подставляя значения напряженностей МП, определяемые формулами (2) и (3), в уравнение (4), получаем следующее равенство:
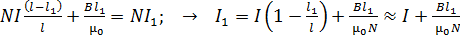 . (5)
. (5)
Здесь учтено, что длина зазора 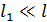 , следовательно,
, следовательно,  .
.
Вычисляем ток в обмотке по формуле (5):
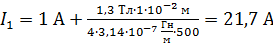 .
.
Таким образом, для намагничивания железного сердечника с воздушным промежутком требуется существенно больший ток, чем в случае сплошного сердечника.
Задача 58. Для сердечника тороида с прорезью, описанного в предыдущей задаче, определите магнитную проницаемость 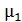 . Сравните величину
. Сравните величину 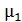 с магнитной проницаемостью
с магнитной проницаемостью 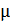 сплошного сердечника того же тороида.
сплошного сердечника того же тороида.
Дано Решение
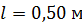 ; ;
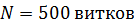 ; ;
 ; ;
 . .
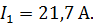

|
В случае сердечника с прорезью запишем теорему о циркуляции вектора 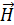 (см. уравнение (4) в решении предыдущей задачи):
(см. уравнение (4) в решении предыдущей задачи):
 . (1)
. (1)
В это уравнение подставим значения напряженностей магнитного поля в сердечнике:  , и в воздушном промежутке –
, и в воздушном промежутке – 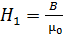 . При этом уравнение (1) принимает следующий вид:
. При этом уравнение (1) принимает следующий вид:
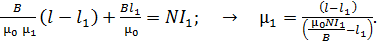 (2)
(2)
Заметим, что полученное выражение (2) является только расчетной формулой величины 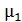 и не передает зависимость
и не передает зависимость 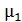 от длины зазора. Вычисляем магнитную проницаемость железного сердечника с воздушным промежутком по формуле (2):
от длины зазора. Вычисляем магнитную проницаемость железного сердечника с воздушным промежутком по формуле (2):
 .
.
Для сплошного железного сердечника из формулы связи величин  :
:  , – определяем магнитную проницаемость сердечника:
, – определяем магнитную проницаемость сердечника:
 (3)
(3)
Необходимое значение напряженности 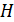 поля, намагничивающего сердечник до величины магнитной индукции
поля, намагничивающего сердечник до величины магнитной индукции  , определяем по графику
, определяем по графику 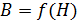 (см. рис. 86):
(см. рис. 86): 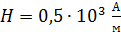 . Используя эти значения
. Используя эти значения  , вычисляем магнитную проницаемость сплошного железного сердечника по формуле (3):
, вычисляем магнитную проницаемость сплошного железного сердечника по формуле (3):
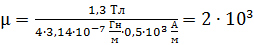 .
.
Таким образом, прорезь длиной  в железном сердечнике вдвое понижает его магнитную проницаемость.
в железном сердечнике вдвое понижает его магнитную проницаемость.
Задача 59. Тонкий кольцевой ферромагнитный сердечник средним радиусом 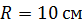 имеет поперечную прорезь длиной
имеет поперечную прорезь длиной  . Сердечник был намагничен током, протекающим по обмотке, после чего ток отключили. Определите, во сколько раз напряженность магнитного поля
. Сердечник был намагничен током, протекающим по обмотке, после чего ток отключили. Определите, во сколько раз напряженность магнитного поля  в воздушном зазоре превышает напряженность
в воздушном зазоре превышает напряженность 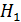 МП в сердечнике. Оцените магнитную проницаемость
МП в сердечнике. Оцените магнитную проницаемость 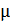 ферромагнитного сердечника.
ферромагнитного сердечника.
Дано Решение
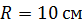 ; ;
 . .


|
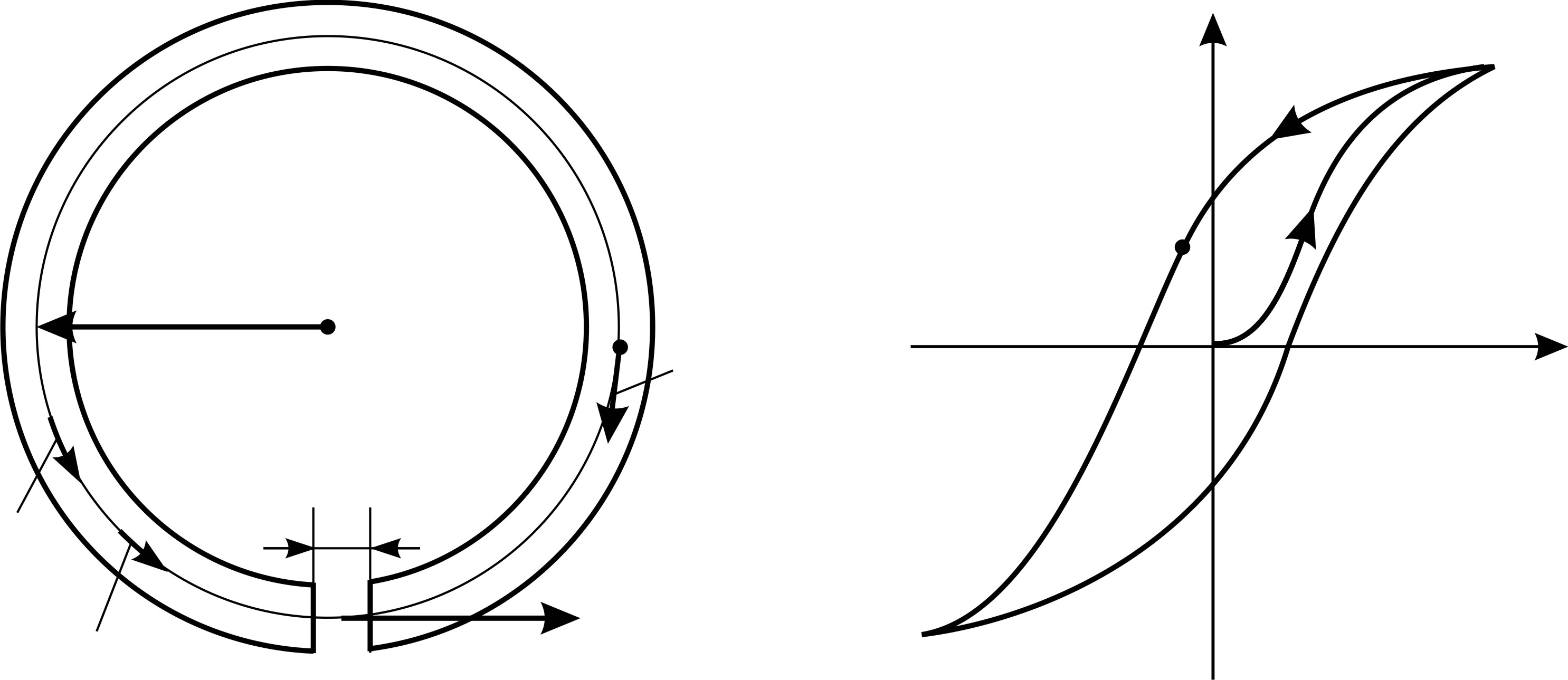
Рис. 89 Рис. 90 |
Запишем теорему о циркуляции вектора 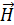 вдоль контура
вдоль контура 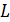 , совпадающего со средней линией сердечника (рис. 89). Направление обхода по контуру интегрирования выберем вдоль вектора магнитной индукции
, совпадающего со средней линией сердечника (рис. 89). Направление обхода по контуру интегрирования выберем вдоль вектора магнитной индукции 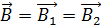 (рассеянием магнитного потока в воздушном зазоре пренебрегаем). Так как ток в обмотке отсутствует:
(рассеянием магнитного потока в воздушном зазоре пренебрегаем). Так как ток в обмотке отсутствует: 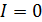 , – то теорема запишется в следующем виде:
, – то теорема запишется в следующем виде:
 (1)
(1)
Здесь проекция вектора напряженности 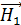 в сердечнике
в сердечнике 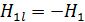 , так как после отключения намагничивающего поля напряженностью
, так как после отключения намагничивающего поля напряженностью 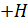 соотношение величин
соотношение величин 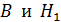 в магнитном поле сердечника соответствует точке
в магнитном поле сердечника соответствует точке 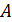 на верхней ветви петли гистерезиса (рис. 90). Из уравнения (1) находим искомое отношение напряженностей:
на верхней ветви петли гистерезиса (рис. 90). Из уравнения (1) находим искомое отношение напряженностей:
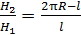 .
.
Вычисляем это отношение, показывающее, во сколько раз напряженность магнитного поля  в воздушном зазоре превышает напряженность
в воздушном зазоре превышает напряженность 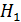 МП в сердечнике:
МП в сердечнике:
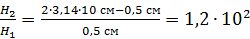 .
.
Для определения магнитной проницаемости 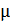 ферромагнитного сердечника используем формулы связи магнитной индукции
ферромагнитного сердечника используем формулы связи магнитной индукции 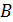 с напряженностью магнитного поля
с напряженностью магнитного поля 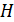 :
:
а) в сердечнике величина  ;
;
б) в зазоре –  , так как для воздуха
, так как для воздуха 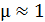 .
.
Приравнивая 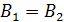 , в силу непрерывности линий магнитной индукции, получаем расчетную формулу магнитной проницаемости сердечника после отключения тока в намагничивающей обмотке:
, в силу непрерывности линий магнитной индукции, получаем расчетную формулу магнитной проницаемости сердечника после отключения тока в намагничивающей обмотке:
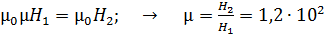 .
.
Задача 60. Тороидальная катушка с железным сердечником, длина осевой линии которого 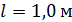 , имеет обмотку, содержащую
, имеет обмотку, содержащую 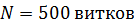 с током
с током 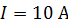 . В сердечнике имеется поперечная прорезь длиной
. В сердечнике имеется поперечная прорезь длиной  (рис. 91). Определите индукцию магнитного поля
(рис. 91). Определите индукцию магнитного поля 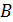 в сердечнике и в зазоре. Рассеянием магнитного потока в зазоре можно пренебречь.
в сердечнике и в зазоре. Рассеянием магнитного потока в зазоре можно пренебречь.
Дано Решение
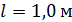 ; ;
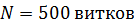 ; ;
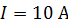 ; ;
 . .
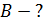
|

Рис. 91 |
Для материала сердечника – железа, величина магнитной индукции 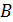 зависит от напряженности магнитного поля
зависит от напряженности магнитного поля 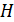 в соответствии с экспериментальной кривой намагничивания
в соответствии с экспериментальной кривой намагничивания  (см. рис. 86). Величина напряженности магнитного поля
(см. рис. 86). Величина напряженности магнитного поля 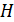 зависит от тока в обмотке катушки. Запишем теорему о циркуляции вектора
зависит от тока в обмотке катушки. Запишем теорему о циркуляции вектора 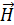 вдоль контура интегрирования
вдоль контура интегрирования 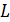 , совпадающего с осевой линией тороидального сердечника (см. рис. 91):
, совпадающего с осевой линией тороидального сердечника (см. рис. 91):
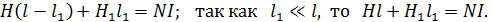 (1)
(1)
Здесь напряженность МП в воздушном зазоре 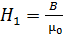 , так как для воздуха
, так как для воздуха 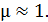 С учетом этого теорему (1) запишем в следующем виде:
С учетом этого теорему (1) запишем в следующем виде:
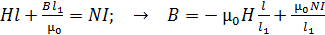 . (2)
. (2)
Получено уравнение прямой линии 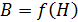 для заданного в задаче тороидального сердечника с воздушным промежутком.
для заданного в задаче тороидального сердечника с воздушным промежутком.
Итак, имеется две зависимости, связывающие переменные  : 1) график кривой намагничивания железа
: 1) график кривой намагничивания железа 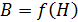 и 2) зависимость
и 2) зависимость 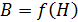 , описываемая уравнением (2). Имея две зависимости, можем определить две неизвестные величины –
, описываемая уравнением (2). Имея две зависимости, можем определить две неизвестные величины –  . Так как одна из зависимостей экспериментальная, и задана графиком, то решим систему двух уравнений
. Так как одна из зависимостей экспериментальная, и задана графиком, то решим систему двух уравнений 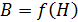 графическим методом. Для этого построим линейную зависимость (2) на поле кривой намагничивания (рис. 92).
графическим методом. Для этого построим линейную зависимость (2) на поле кривой намагничивания (рис. 92).
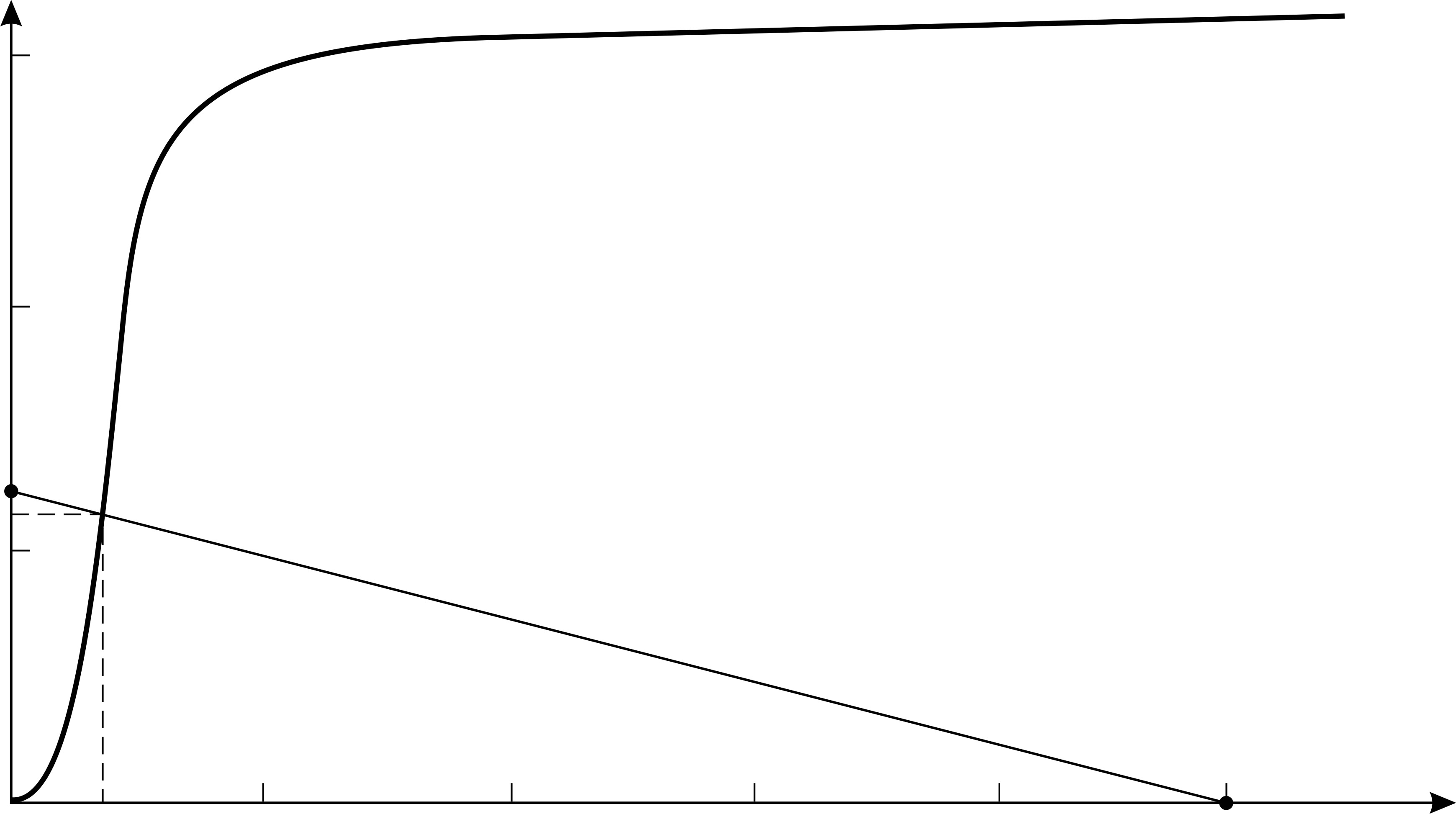
Рис. 92 |
Для проведения прямой линии достаточно знать две точки; их координаты определим по уравнению (2), выбрав удобные для вычислений точки: одна из них – точка 1, координаты которой равны 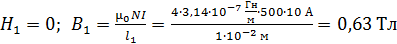 ; вторая – точка 2:
; вторая – точка 2: 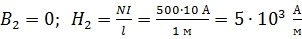 . Эти точки с вычисленными координатами: т. 1 (0; 0,63 Тл) и т. 2 (
. Эти точки с вычисленными координатами: т. 1 (0; 0,63 Тл) и т. 2 (  ; 0), – нанесем на поле графика и проведем прямую 1–2, которая описывается уравнением (2). Решением системы двух зависимостей, представленных на графике, является их общая точка – точка пересечения линий. Эта точка имеет следующие координаты (см. рис. 92):
; 0), – нанесем на поле графика и проведем прямую 1–2, которая описывается уравнением (2). Решением системы двух зависимостей, представленных на графике, является их общая точка – точка пересечения линий. Эта точка имеет следующие координаты (см. рис. 92): 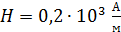 ;
; 
Дата добавления: 2016-10-07; просмотров: 3908;

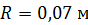 ;
;