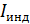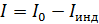Индуктивность цепи. Энергия магнитного поля
Основной закон электромагнитной индукции (ЭМИ) – закон Фарадея: электродвижущая сила индукции 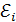 равна скорости изменения магнитного потока сквозь площадь контура:
равна скорости изменения магнитного потока сквозь площадь контура:
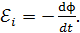 (24)
(24)
В каждом витке обмотки соленоида или тороида возникает ЭДС индукции, равная 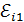 ; так как витки одинаковы и соединены последовательно, то ЭДС индукции, возникающая в катушке, равна сумме ЭДС
; так как витки одинаковы и соединены последовательно, то ЭДС индукции, возникающая в катушке, равна сумме ЭДС 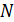 витков:
витков:
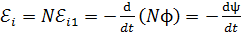 , (25)
, (25)
где 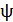 – потокосцепление контура.
– потокосцепление контура.
Частные случаи применения закона электромагнитной индукции (25):
1) при поступательном движении проводника длиной 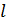
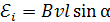 , (26)
, (26)
где 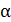 – угол между векторами скорости проводника
– угол между векторами скорости проводника  и магнитной индукции
и магнитной индукции 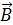 ;
;
2) при вращении рамки в однородном МП с индукцией 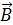
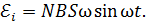 (27)
(27)
Здесь 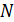 – число витков рамки;
– число витков рамки; 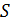 – площадь витка;
– площадь витка; 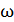 – угловая скорость вращения;
– угловая скорость вращения; 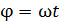 – угол поворота нормали рамки
– угол поворота нормали рамки 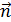 в момент времени
в момент времени 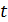 (при
(при 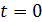 вектор
вектор 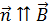 ).
).
Количество электричества 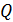 , протекающее через сечение проводника сопротивлением
, протекающее через сечение проводника сопротивлением  при изменении потокосцепления
при изменении потокосцепления 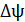 , определяется формулой
, определяется формулой
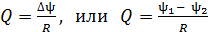 , (28)
, (28)
где 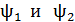 – потокосцепления контура в начальном и конечном положениях.
– потокосцепления контура в начальном и конечном положениях.
Заметим, что при решении задач контрольной работы №4 формулы (26), (27) и (28) следует выводить, исходя из основного закона ЭМИ (25).
Полный магнитный поток 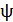 контура пропорционален току
контура пропорционален току 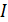 в этом контуре:
в этом контуре:
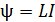 , (29)
, (29)
где 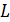 – коэффициент пропорциональности, называемый индуктивностью контура. Индуктивность длинного соленоида и тороида определяется формулой
– коэффициент пропорциональности, называемый индуктивностью контура. Индуктивность длинного соленоида и тороида определяется формулой
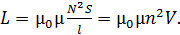 (30)
(30)
Здесь 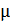 – магнитная проницаемость сердечника;
– магнитная проницаемость сердечника; 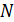 – число витков катушки;
– число витков катушки; 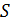 – площадь поперечного сечения сердечника (площадь витка);
– площадь поперечного сечения сердечника (площадь витка); 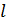 – длина сердечника;
– длина сердечника; 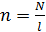 – число витков на единицу длины соленоида;
– число витков на единицу длины соленоида; 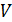 – объем сердечника.
– объем сердечника.
ЭДС самоиндукции 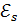 , возникающая в контуре при изменении в нем тока, в случае постоянной индуктивности контура
, возникающая в контуре при изменении в нем тока, в случае постоянной индуктивности контура 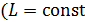 , если сердечник катушки неферромагнитный) изменяется по закону:
, если сердечник катушки неферромагнитный) изменяется по закону:
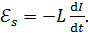 (31)
(31)
|
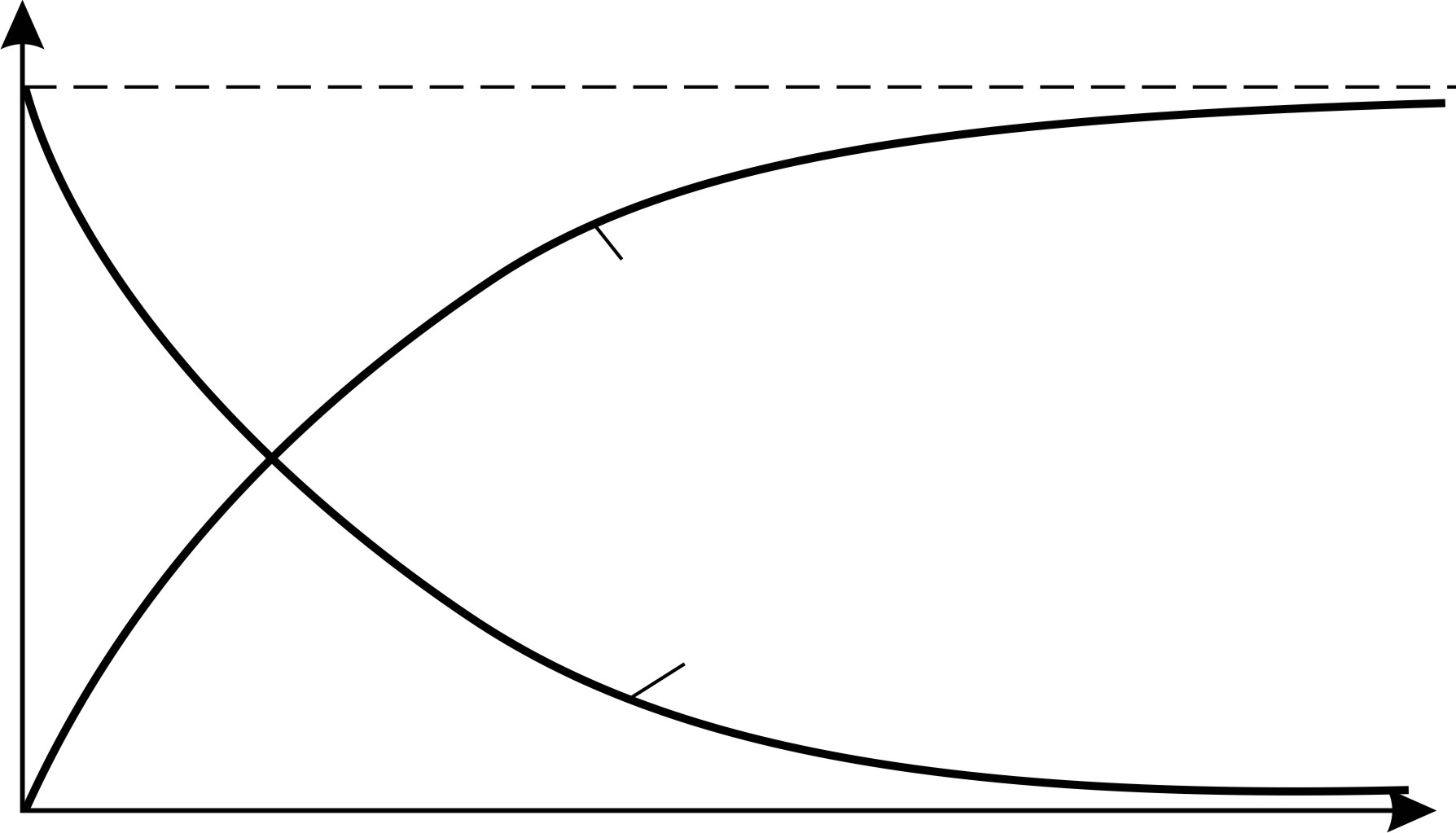
Рис. 56 |

|
 и индуктивность
и индуктивность 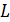 , ток изменяется с течением времени
, ток изменяется с течением времени 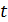 по следующему закону:
по следующему закону:
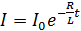 , (32)
, (32)
где  – ток в момент времени
– ток в момент времени 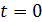 .
.
Ток, определяемый формулой (32), является индукционным; в соответствии с законом Ома, величина этого тока в любой момент времени 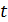 :
: 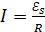 , где ЭДС самоиндукции
, где ЭДС самоиндукции 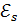 определяется законом ЭМИ (31).
определяется законом ЭМИ (31).
При подключении цепи к источнику тока ЭДС самоиндукции создает индукционный ток, препятствующий нарастанию тока до значения  . В результате ток в цепи устанавливается с течением времени по закону
. В результате ток в цепи устанавливается с течением времени по закону
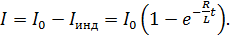 (33)
(33)
Здесь, согласно закону Ома, ток 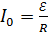 , где
, где 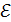 – ЭДС источника тока.
– ЭДС источника тока.
Энергия 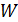 магнитного поля, которое создается током
магнитного поля, которое создается током 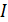 в контуре с индуктивностью
в контуре с индуктивностью 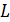 , вычисляется по следующей формуле:
, вычисляется по следующей формуле:
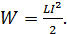 (34)
(34)
Объемная плотность энергии однородного МП 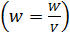 с магнитной индукцией
с магнитной индукцией 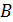 , например, в сердечнике длинного соленоида, определяется формулой
, например, в сердечнике длинного соленоида, определяется формулой
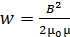 , (35)
, (35)
где 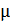 – магнитная проницаемость сердечника.
– магнитная проницаемость сердечника.
Дата добавления: 2016-10-07; просмотров: 1710;