Активность радиоактивного вещества
Активность 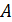 радиоактивного вещества (нуклида) – это скорость его распада, т. е. число распадов за время 1 с:
радиоактивного вещества (нуклида) – это скорость его распада, т. е. число распадов за время 1 с:
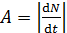 . (17)
. (17)
В СИ единица измерения активности – беккерель (Бк): 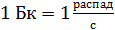 . Кроме того, в ядерной физике используется внесистемная единица активности – кюри (Ки):
. Кроме того, в ядерной физике используется внесистемная единица активности – кюри (Ки): 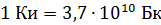 .
.
С учетом закона радиоактивного распада (12) формулу (17) для величины активности можно записать в следующем виде:
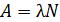 . (18)
. (18)
Таким образом, активность радиоактивного вещества в данный момент времени 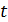 пропорциональна числу ядер
пропорциональна числу ядер 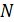 , не распавшихся к этому моменту времени.
, не распавшихся к этому моменту времени.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
План решения задач по теме «Атомное ядро, энергия связи, энергия ядерной реакции»
1. Обратите внимание на единицу энергии, которая используется для энергии связи 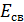 ядра в ядерной физике: 1 МэВ, – соответственно, единица удельной энергии связи
ядра в ядерной физике: 1 МэВ, – соответственно, единица удельной энергии связи 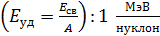 .
.
2. Чтобы получить энергию связи в мегаэлектрон-вольтах (при вычислении по формуле 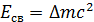 ), массы атомов из справочной таблицы берут в атомных единицах массы (а.е.м.). Учитывая, что
), массы атомов из справочной таблицы берут в атомных единицах массы (а.е.м.). Учитывая, что 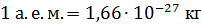 , получим:
, получим:
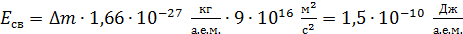 .
.
Так как 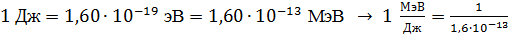 , то
, то
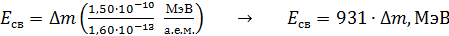 .
.
Последняя формула является наиболее удобной для вычисления энергии связи ядра и энергии ядерной реакции в единицах 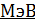 ; при этом дефект массы
; при этом дефект массы 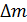 выражают в
выражают в 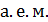
3. Отметим, что при вычислении дефекта массы ядра 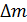 , а также разности масс
, а также разности масс 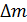 при расчете энергии ядерной реакции по формуле (10), следует брать массы атомов с указанием всех значащих цифр, приведенных в справочной таблице. Но полученные значения
при расчете энергии ядерной реакции по формуле (10), следует брать массы атомов с указанием всех значащих цифр, приведенных в справочной таблице. Но полученные значения 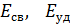 и теплового эффекта ядерной реакции
и теплового эффекта ядерной реакции 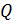 следует округлять, как обычно, до 3-х значащих цифр (так как с такой точностью найдено число
следует округлять, как обычно, до 3-х значащих цифр (так как с такой точностью найдено число 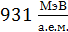 в расчетной формуле).
в расчетной формуле).
4. При вычислении энергии ядерной реакции по формуле (10):
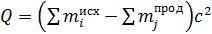 ;
; 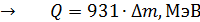
знак величины 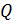 определяется знаком разности масс
определяется знаком разности масс 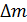 : если
: если 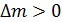 , т. е.
, т. е. 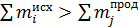 , то энергия выделяется и величина
, то энергия выделяется и величина 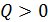 ; если
; если 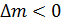 , то энергия ядерной реакции отрицательна – энергия поглощается в ходе реакции.
, то энергия ядерной реакции отрицательна – энергия поглощается в ходе реакции.
Задача 40. Вычислите энергию связи 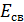 ядер атомов гелия
ядер атомов гелия 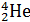 и алюминия
и алюминия 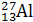 и их удельную энергию связи
и их удельную энергию связи 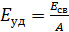 . Определите, какое ядро прочнее.
. Определите, какое ядро прочнее.
Дано
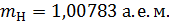 ; ;
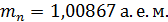 ; ;
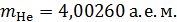 ; ;
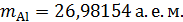 . .
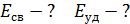 Какое ядро прочнее?
Какое ядро прочнее?
| Решение
Определяем энергию связи ядра по формуле
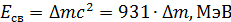 , (1)
где дефект массы при образовании ядра , (1)
где дефект массы при образовании ядра
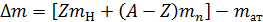 . (2)
Здесь . (2)
Здесь 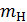 – масса атома водорода; – масса атома водорода; 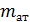 – масса атома; – масса атома; 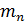 – масса нейтрона; – масса нейтрона; 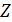 – порядковый номер элемента в таблице Д.И. Менделеева; – порядковый номер элемента в таблице Д.И. Менделеева; 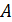 – массовое число. – массовое число.
|
1) Вычисляем для ядра атома гелия 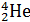 :
: 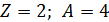 .
.
Дефект массы – по формуле (2):
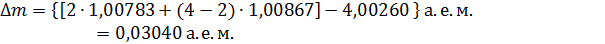
Энергия связи ядра гелия – по формуле (1):
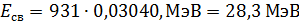 .
.
Удельная энергия связи
 .
.
2) Аналогично вычисляем для ядра алюминия 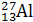 :
: 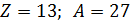 .
.
Дефект массы – по формуле (2):
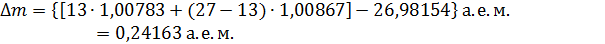
Энергия связи ядра гелия – по формуле (1):
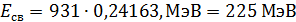 .
.
Удельная энергия связи
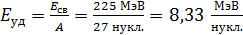 .
.
Определим, какое из этих двух ядер прочнее. Чтобы «развалить» ядро, достаточно отделить от него лишь один нуклон, – при этом образуется ядро другого атома, с массовым числом ( 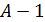 ). Меньшая энергия для этого процесса
). Меньшая энергия для этого процесса 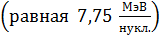 потребуется ядру атома гелия, так как его удельная энергия связи
потребуется ядру атома гелия, так как его удельная энергия связи 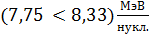
Задача 41. Определите энергию 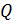 , которая выделяется при реакции
, которая выделяется при реакции
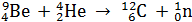 .
.
Дано
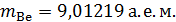 ; ;
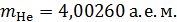 ; ;
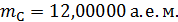 ; ;
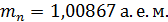 . .
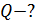
| Решение
Определяем энергию ядерной реакции по формуле
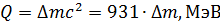 , (1)
где , (1)
где 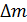 – разность масс исходных ядер и ядер продуктов реакции: – разность масс исходных ядер и ядер продуктов реакции:
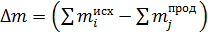 . (2) . (2)
|
Разность масс ядер в уравнении (2) равна разности масс соответствующих атомов 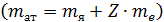 , так как, согласно закону сохранения электрического заряда:
, так как, согласно закону сохранения электрического заряда: 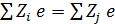 , – сумма зарядовых чисел исходных ядер и продуктов реакции одинакова. Для данной в задаче реакции уравнение (2) запишем в следующем виде:
, – сумма зарядовых чисел исходных ядер и продуктов реакции одинакова. Для данной в задаче реакции уравнение (2) запишем в следующем виде:
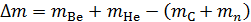 . (3)
. (3)
По этой формуле вычисляем разность масс атомов:
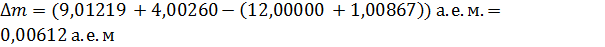 .
.
Величина 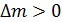 , т. е.
, т. е. 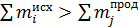 ; следовательно,
; следовательно, 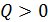 и энергия выделяется. Энергию, которая выделяется при протекании реакции, вычисляем по формуле (1):
и энергия выделяется. Энергию, которая выделяется при протекании реакции, вычисляем по формуле (1):
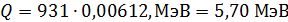 .
.
7.2. План решения задач по теме «Радиоактивность»
1. Скорость распада и активность 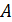 радиоактивного вещества зависят от постоянной распада
радиоактивного вещества зависят от постоянной распада 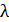 данного вещества; ее находят, используя табличное значение периода полураспада
данного вещества; ее находят, используя табличное значение периода полураспада 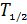 с помощью формулы
с помощью формулы
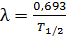 . (1)
. (1)
2. Активность 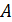 радиоактивного вещества в данный момент времени
радиоактивного вещества в данный момент времени 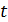 зависит также от концентрации нераспавшихся ядер
зависит также от концентрации нераспавшихся ядер 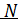 , которуюнаходят с помощью закона радиоактивного распада:
, которуюнаходят с помощью закона радиоактивного распада:
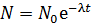 . (2)
. (2)
3. Если необходимо найти число распавшихся ядер 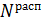 , то используют очевидное равенство для начального количества ядер в образце:
, то используют очевидное равенство для начального количества ядер в образце:

где 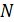 – число нераспавшихся ядер, оно определяется законом распада (2).
– число нераспавшихся ядер, оно определяется законом распада (2).
Задача 42. Определите, какая доля радиоактивного изотопа йода
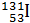 распадается в течение времени
распадается в течение времени 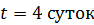 .
.
Дано
Йод 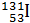 : : 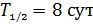 ; ;
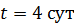 . .
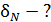
| Решение
Доля распавшихся ядер – это отношение числа распавшихся ядер 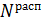 к начальному числу ядер к начальному числу ядер 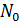 : : 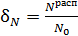 . А закон радиоактивного распада дает число ядер . А закон радиоактивного распада дает число ядер 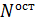 – оставшихся к моменту времени – оставшихся к моменту времени 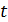 : :
|
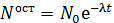 . (1)
. (1)
Так как 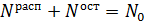 , то запишем
, то запишем 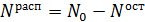 и выразим долю:
и выразим долю:
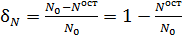 . (2)
. (2)
С учетом закона радиоактивного распада (2) получаем формулу:
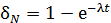 . (3)
. (3)
Здесь постоянная распада 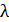 и период полураспада
и период полураспада 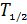 радиоактивного вещества связаны следующим соотношением:
радиоактивного вещества связаны следующим соотношением:
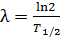 . (4)
. (4)
Подставляя величину 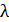 по формуле (4) в уравнение (3), получаем расчетную формулу в виде:
по формуле (4) в уравнение (3), получаем расчетную формулу в виде:
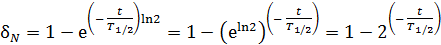 .
.
Вычисляем по полученной формуле долю ядер, распавшихся к моменту времени 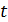 :
:
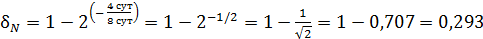 .
. 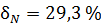 .
.
Задача 43. Для образца радиоактивного изотопа иридия 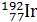 , начальная масса которого
, начальная масса которого 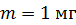 , определите число ядер
, определите число ядер 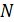 , распавшихся в течение времени: 1)
, распавшихся в течение времени: 1) 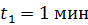 ; 2)
; 2) 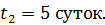
Дано
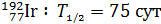 ; ;
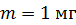 ; ;
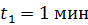 ; ;
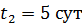 . .

| Решение
Найдем начальное число атомов 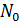 в образце, содержащем число молей в образце, содержащем число молей 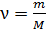 : :
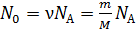 , (1)
где , (1)
где 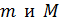 – масса и молярная масса иридия – масса и молярная масса иридия 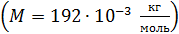 ; ; 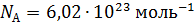 – число Авогадро (число атомов в одном моле вещества). – число Авогадро (число атомов в одном моле вещества).
|
Закон радиоактивного распада ядер можно записать в двух формах:
1) В дифференциальной записи – для малого числа ядер 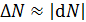 , распавшихся за малое (по сравнению с периодом полураспада
, распавшихся за малое (по сравнению с периодом полураспада 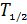 ) время
) время 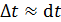 :
:
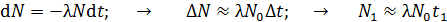 . (2)
. (2)
Эту формулу закона можно применить для промежутка времени 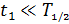 .
.
2) В интегральной форме – для времени распада, соизмеримого с величиной 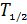 :
:
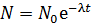 . (3)
. (3)
Здесь 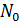 – начальное число ядер (в момент времени
– начальное число ядер (в момент времени 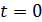 );
); 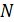 – число нераспавшихся ядер в момент времени
– число нераспавшихся ядер в момент времени 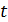 ;
; 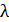 – постоянная радиоактивного распада.
– постоянная радиоактивного распада.
Закон распада в форме (3) применим для промежутка времени 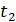 . Так как число распавшихся ядер
. Так как число распавшихся ядер 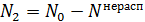 , то, с учетом закона (3):
, то, с учетом закона (3):
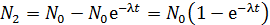 . (4)
. (4)
В уравнениях (2) и (4) постоянная распада 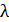 и период полураспада
и период полураспада 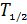 радиоактивного вещества связаны следующим соотношением:
радиоактивного вещества связаны следующим соотношением:
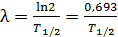 . (5)
. (5)
С учетом формул (1) и (5) преобразуем уравнения (2) и (4) в следующие расчетные формулы:
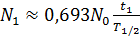 . (6)
. (6)
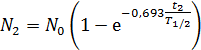 . (7)
. (7)
Вычислим начальное число ядер в образце:
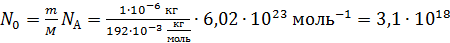 .
.
Вычисляем по формуле (6) число ядер, распавшихся за время 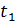 :
:
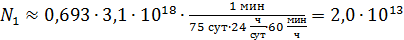 .
.
Полученное число 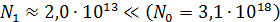 , что подтверждает правомерность использования простой приближенной формулы (2) закона радиоактивного распада.
, что подтверждает правомерность использования простой приближенной формулы (2) закона радиоактивного распада.
По формуле (7) вычисляем число ядер, распавшихся за время 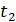 :
:
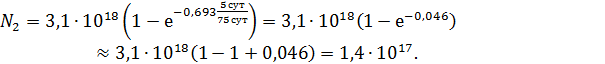
Здесь использовали формулу для приближенного вычисления при 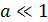 :
:
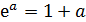 .
.
Задача 44. Активность 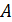 образца некоторого изотопа за время
образца некоторого изотопа за время 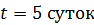 уменьшилась на 20%. Определите период полураспада
уменьшилась на 20%. Определите период полураспада 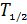 этого изотопа.
этого изотопа.
Дано
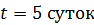 ; ;
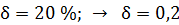 . .
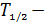 ? ?
| Решение
В задаче дано относительное уменьшение активности образца:
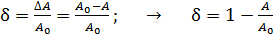 , (1) , (1)
|
где 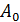 – активность образца в начальный момент времени
– активность образца в начальный момент времени 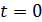 ;
; 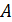 – активность того же образца в момент времени
– активность того же образца в момент времени 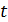 .
.
Активность радиоактивного вещества пропорциональна числу ядер, которые будут распадаться, т. е. числу 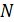 нераспавшихся ядер:
нераспавшихся ядер:
 . (2)
. (2)
По закону радиоактивного распада число 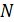 нераспавшихся ядер
нераспавшихся ядер
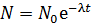 . (3)
. (3)
Следовательно, формула (2), с учетом закона (3), приводит к зависимости активности образца от времени 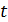 в виде:
в виде:
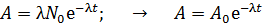 . (4)
. (4)
Подставляя зависимость (4) в формулу (1), получаем следующую формулу:
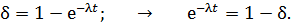
Логарифмируя, находим
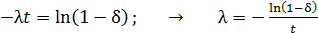 . (5)
. (5)
Период полураспада 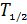 и постоянная распада
и постоянная распада 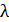 радиоактивного вещества связаны следующим соотношением:
радиоактивного вещества связаны следующим соотношением:
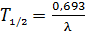 . (6)
. (6)
Подставляя в последнюю формулу выражение (5), получаем расчетную формулу в следующем виде:
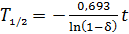 .
.
Вычисляем период полураспада радиоактивного вещества:
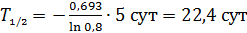 .
.
Задача 45. Определите массу 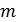 образца радиоактивного изотопа актиния
образца радиоактивного изотопа актиния 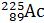 , имеющего активность
, имеющего активность 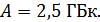
Дано
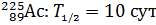 ; ;
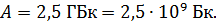
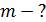
| Решение
Активность 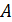 радиоактивного образца пропорциональна числу радиоактивного образца пропорциональна числу 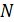 нераспавшихся ядер в этом образце: нераспавшихся ядер в этом образце:
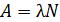 , (1)
где , (1)
где 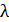 – постоянная распада данного вещества. – постоянная распада данного вещества.
|
Постоянная распада 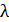 и период полураспада
и период полураспада 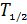 радиоактивного вещества связаны следующим соотношением:
радиоактивного вещества связаны следующим соотношением:
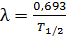 . (2)
. (2)
Из формулы (1) выразим число ядер в образце и учтем выражение (2):
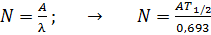 . (3)
. (3)
Число ядер равно числу атомов изотопа актиния, поэтому можно найти число молей 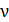 радиоактивного вещества в образце по формуле:
радиоактивного вещества в образце по формуле:
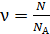 , (4)
, (4)
где 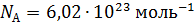 – число Авогадро (число атомов в одном моле вещества). С другой стороны, число молей вещества можно выразить через его массу
– число Авогадро (число атомов в одном моле вещества). С другой стороны, число молей вещества можно выразить через его массу 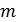 и молярную массу актиния
и молярную массу актиния 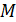
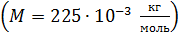 :
:
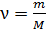 . (5)
. (5)
Приравнивая величину 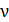 по формулам (4) и (5) и учитывая равенство (3), получаем расчетную формулу массы образца:
по формулам (4) и (5) и учитывая равенство (3), получаем расчетную формулу массы образца:
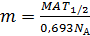 . (6)
. (6)
Здесь период полураспада следует выразить в секундах, так как единица активности 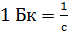 .
.
Вычисляем массу образца радиоактивного вещества по формуле (6):
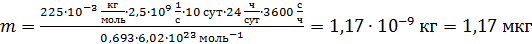 .
.
Задача 46. Счетчик 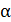 -частиц, установленный вблизи образца радиоактивного изотопа, при первом измерении зарегистрировал
-частиц, установленный вблизи образца радиоактивного изотопа, при первом измерении зарегистрировал 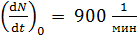 – частиц в минуту, а через время
– частиц в минуту, а через время 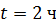 –
– 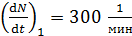 . Определите период полураспада изотопа
. Определите период полураспада изотопа 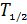 .
.
Дано
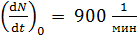 ; ;
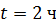 ; ;
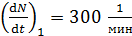 . .
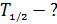
| Решение
В условии задачи дана скорость распада радиоактивного изотопа в два момента времени: 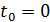 и и 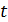 . Скорость распада дает нам активность изотопа . Скорость распада дает нам активность изотопа 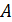 : :
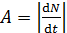 . (1)
Величина . (1)
Величина 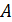 пропорциональна числу пропорциональна числу 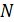 нераспавшихся ядер в этом образце: нераспавшихся ядер в этом образце:
 . (2) . (2)
|
Число 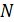 нераспавшихся ядер определяем по закону радиоактивного распада:
нераспавшихся ядер определяем по закону радиоактивного распада:
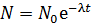 . (3)
. (3)
Заменяя в уравнении (3) 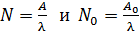 (в соответствии с формулами (2)), получаем соотношение активностей радиоактивного образца в виде:
(в соответствии с формулами (2)), получаем соотношение активностей радиоактивного образца в виде:
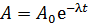 . (4)
. (4)
Здесь постоянная распада 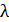 связана с периодом полураспада
связана с периодом полураспада 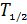 радиоактивного вещества связаны следующим соотношением:
радиоактивного вещества связаны следующим соотношением:
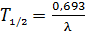 . (5)
. (5)
Найдем величину 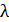 из уравнения (4) путем его логарифмирования:
из уравнения (4) путем его логарифмирования:
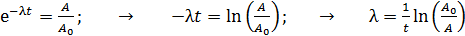 . (6)
. (6)
Подставляя найденную величину 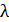 в формулу (5), получаем расчетную формулу периода полураспада
в формулу (5), получаем расчетную формулу периода полураспада 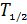 :
:
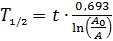 . (7)
. (7)
Вычисляем период полураспада 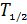 радиоактивного изотопа, заменяя отношение активностей образца (на основании формулы (1)), отношением измеренных счетчиком скоростей
радиоактивного изотопа, заменяя отношение активностей образца (на основании формулы (1)), отношением измеренных счетчиком скоростей 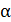 -распада ядер радиоактивного изотопа:
-распада ядер радиоактивного изотопа:
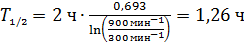 .
.
Задача 47. Определите период полураспада изотопа 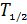 , если известно, что из миллиона атомов
, если известно, что из миллиона атомов 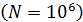 этого радиоактивного изотопа за каждую секунду распадаются ядра
этого радиоактивного изотопа за каждую секунду распадаются ядра 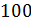 атомов:
атомов: 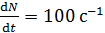 .
.
Дано
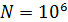 ; ;
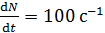 . .
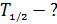
| Решение
В условии задачи дана скорость распада радиоактивного изотопа, равная активности изотопа 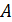 : :
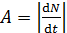 . (1)
Величина . (1)
Величина 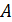 пропорциональна числу пропорциональна числу 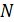 нераспавшихся ядер в этом образце: нераспавшихся ядер в этом образце:
|
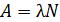 . (2)
. (2)
Приравнивая активности 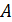 образца в формулах (1) и (2), получаем выражение для определения постоянной
образца в формулах (1) и (2), получаем выражение для определения постоянной 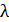 радиоактивного распада изотопа:
радиоактивного распада изотопа:
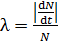 . (3)
. (3)
Период полураспада 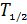 и постоянная распада
и постоянная распада 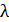 радиоактивного вещества связаны следующим соотношением:
радиоактивного вещества связаны следующим соотношением:
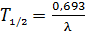 . (4)
. (4)
Подставляя в последнее равенство величину 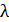 по формуле (3), получаем расчетную формулу периода полураспада
по формуле (3), получаем расчетную формулу периода полураспада 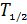 радиоактивного изотопа:
радиоактивного изотопа:
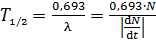 .
.
Вычисляем величину периода полураспада:
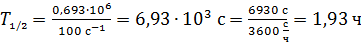 .
.
Дата добавления: 2016-10-07; просмотров: 14754;











