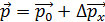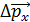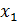Соотношение неопределенностей
В классической механике частица движется по определенной траектории; при этом в любой момент времени можно точно определить ее координаты 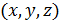 и импульс
и импульс 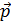 (проекции
(проекции 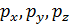 ).
).
В микромире, который описывает квантовая механика, благодаря волновым свойствам частиц, проявляются ограничения для некоторых величин (см. далее п. 1, 1а и 2).
1) Соотношение неопределенностей Гейзенберга: микрочастица (например, электрон) не может одновременно иметь точные значения двух величин: координаты 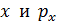 – соответствующей проекции импульса, (а также
– соответствующей проекции импульса, (а также 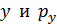 ;
; 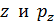 ). Неопределенности этих величин связаны следующими соотношениями:
). Неопределенности этих величин связаны следующими соотношениями:
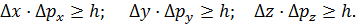 (12)
(12)
Таким образом, произведение неопределенности координаты 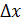 и неопределенности проекции импульса
и неопределенности проекции импульса 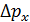 не может быть меньше, чем
не может быть меньше, чем 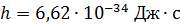 , т. е. при увеличении
, т. е. при увеличении 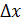 уменьшается
уменьшается 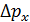 .
.
То, что это обусловлено волновыми свойствами частиц, видно из опыта по дифракции пучка электронов на щели шириной 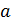 (рис. 50).
(рис. 50).
|
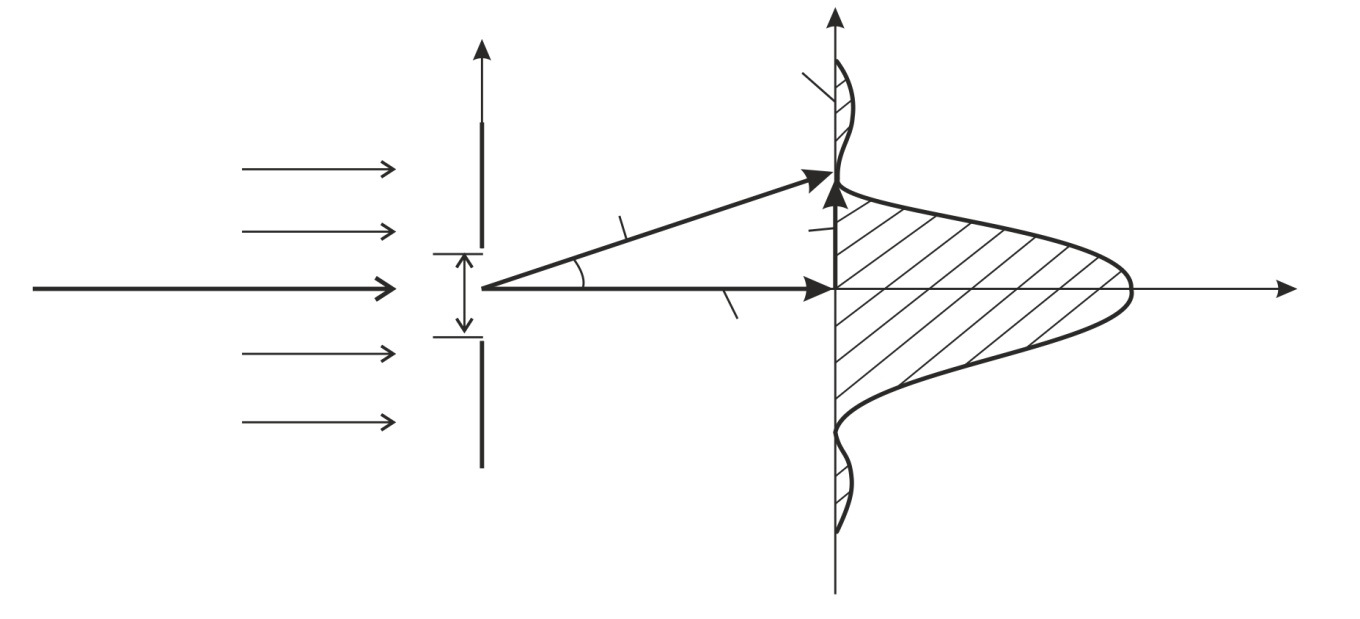
Рис. 50 |
До щели электрон имел импульс 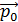 – точное значение в параллельном пучке электронов, т. е.
– точное значение в параллельном пучке электронов, т. е. 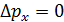 . Но при этом координата
. Но при этом координата  электрона в пучке была любая:
электрона в пучке была любая: 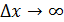 (точнее
(точнее 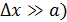 .
.
После щели стала известна координата электрона, прошедшего щель: 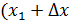 ) (см. рис. 50), где
) (см. рис. 50), где 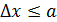 , т. е. с точностью до ширины щели
, т. е. с точностью до ширины щели 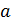 . Но на экране, по графику распределения интенсивности
. Но на экране, по графику распределения интенсивности 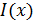 пучка электронов, видим дифракционное расхождение пучка, так как появилась составляющая импульса
пучка электронов, видим дифракционное расхождение пучка, так как появилась составляющая импульса 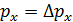 . Приравнивая значение
. Приравнивая значение 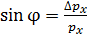 (по треугольнику на рисунке) и по условию первого дифракционного минимума на щели:
(по треугольнику на рисунке) и по условию первого дифракционного минимума на щели: 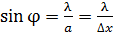 , где
, где 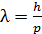 – длина волны электрона, получаем соотношение неопределенностей –
– длина волны электрона, получаем соотношение неопределенностей – 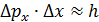 .
.
1а) Неопределенность импульса частицы 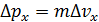 проявляется в неопределенности скорости частицы
проявляется в неопределенности скорости частицы 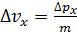 . Оценим минимальную неопределенность скорости частиц:
. Оценим минимальную неопределенность скорости частиц:
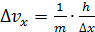 . (13)
. (13)
Для пылинки массой 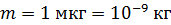 , координата которой известна с неопределенностью
, координата которой известна с неопределенностью 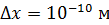 , величина
, величина 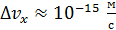 ; такая неопределенность незаметна, так как даже для малой скорости
; такая неопределенность незаметна, так как даже для малой скорости 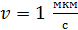 величина
величина 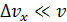 .
.
Из формулы (13) следует, что неопределенность 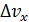 растет с уменьшением массы частицы и для электрона (
растет с уменьшением массы частицы и для электрона ( 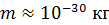 ) величина
) величина 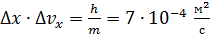 . Так, для электронного луча, толщиной
. Так, для электронного луча, толщиной 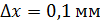 , распространяющегося вдоль оси
, распространяющегося вдоль оси  , величина
, величина 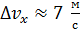 ; эта поперечная лучу скорость
; эта поперечная лучу скорость 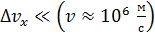 . Следовательно, траектория электрона в пучке (его трек) – это линия, параллельная оси
. Следовательно, траектория электрона в пучке (его трек) – это линия, параллельная оси 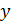 , она не размывается из-за волновых свойств электрона.
, она не размывается из-за волновых свойств электрона.
Иначе ведет себя электрон в атоме, где неопределенность координаты 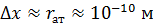 . Для такого электрона
. Для такого электрона 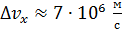 , а его скорость, например, в атоме водорода,
, а его скорость, например, в атоме водорода, 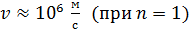 , т. е.
, т. е. 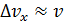 . Поскольку вектор
. Поскольку вектор 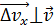 , то траектория электрона в атоме не имеет определенной формы, она не является замкнутой линией.
, то траектория электрона в атоме не имеет определенной формы, она не является замкнутой линией.
2) Соотношение неопределенностей для энергии и времени:
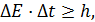 (14)
(14)
где 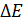 – неопределенность энергии какого-либо состояния частицы с энергией
– неопределенность энергии какого-либо состояния частицы с энергией 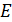 ;
; 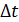 – время существования этого энергетического состояния, или время жизни системы с энергией
– время существования этого энергетического состояния, или время жизни системы с энергией 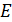 .
.
Атом в основном состоянии существует сколь угодно долго: 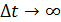 , - поэтому
, - поэтому 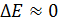 (энергетический уровень основного состояния узкий). Но в возбужденном состоянии время жизни атома
(энергетический уровень основного состояния узкий). Но в возбужденном состоянии время жизни атома 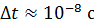 ; тогда по формуле (14) получаем
; тогда по формуле (14) получаем 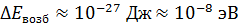 – это ширина размытого возбужденного уровня энергии. В результате энергия фотона, излучаемого при переходе электрона с такого уровня, имеет неопределенность
– это ширина размытого возбужденного уровня энергии. В результате энергия фотона, излучаемого при переходе электрона с такого уровня, имеет неопределенность
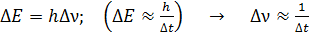 . (15)
. (15)
Эта, так называемая, естественная ширина спектральной линии 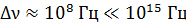 – частоты
– частоты 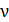 линий оптических спектров. Так как длина волны
линий оптических спектров. Так как длина волны 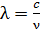 , то, дифференцируя, имеем
, то, дифференцируя, имеем 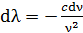 ; принимая, что
; принимая, что 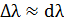 и
и 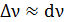 , получаем соотношение
, получаем соотношение 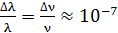 . Такова монохроматичность
. Такова монохроматичность 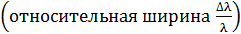 спектральной линии. По величине
спектральной линии. По величине 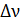 линии спектра, используя формулу (15), можно определить
линии спектра, используя формулу (15), можно определить 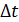 – время жизни атома в возбужденном состоянии.
– время жизни атома в возбужденном состоянии.
Дата добавления: 2016-10-07; просмотров: 3028;

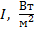 .
.