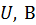Уравнение Эйнштейна для внешнего фотоэффекта

Основные положения квантовой теории фотоэффекта следующие.

1) Свет распространяется и поглощается веществом квантами – фотонами; энергия фотона

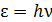, или .

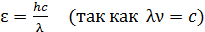2) Фотоэффект – абсолютно неупругое соударение двух частиц: фотона и свободного электрона в металле (Ме), – осуществляется по схеме:

.

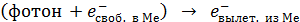Для такого взаимодействия запишем закон сохранения энергии (ЗСЭ):

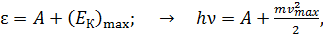(36)

где 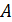– работа выхода свободного электрона из металла, в котором потенциальная энергия свободных электронов отрицательна 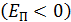, так как они находятся в электростатическом поле положительно заряженных ионов кристалла; 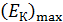– максимальная кинетическая энергия фотоэлектронов, вылетевших из металла. Так как в справочных таблицах приводится минимальное значение работы выхода электрона 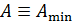(с верхних энергетических уровней зоны проводимости металла), то по уравнению (36) вычисляется только максимальная кинетическая энергия электронов 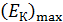, в то время как электроны вылетают из катода с различными скоростями (о чем свидетельствует плавное уменьшение тока по мере увеличения задерживающего потенциала: см. ВАХ на рис. 28).

Уравнение (36) называют уравнением Эйнштейна для внешнего фотоэффекта. Квантовая теория объясняет закономерности фотоэффекта следующим образом.

1) Закон Столетова: 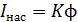, – фототок 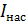, и световой поток 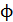определяется потоком частиц 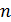– соответственно, числом падающих фотонов 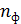и числом вылетевших электронов 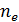за 1 секунду:

; .

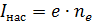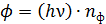Согласно квантовому механизму фотоэффекта, один фотон может выбить только один электрон, поэтому

,

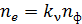где 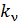– коэффициент пропорциональности, зависящий от частоты света; он мал 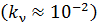т. е. лишь 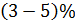фотонов вызывают эмиссию электронов. С учетом записанных соотношений получаем закон Столетова:

.

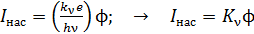2) Граничная частота 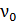(красная граница фотоэффекта) согласно уравнению (36), соответствует 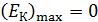; при этом, так как 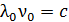, то

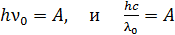. (37)

3) Зависимость кинетической энергии электронов от частоты: 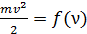. Максимальную кинетическую энергию электронов 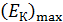измеряют по приложенному задерживающему напряжению , при котором задерживающее электрическое поле уменьшает кинетическую энергию электрона до нуля. Работа этого поля

.

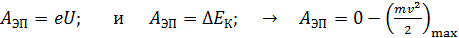Из этих формул получаем, что

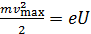, (38)

где 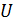– задерживающее напряжение.

С учетом соотношения (38) уравнение Эйнштейна (36) принимает вид:

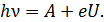(39)

Из уравнения (39) следует линейная зависимость задерживающего напряжения 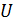от частоты света 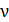, падающего на фотокатод:

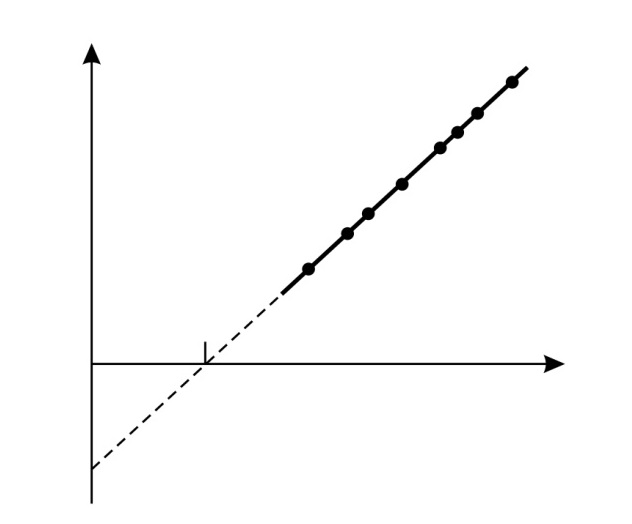
Рис. 29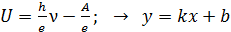

. (40) Уравнение (40) – это уравнение прямой линии с угловым коэффициентом 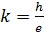. Определение постоянной Планка по угловому коэффициенту экспериментальной линейной зависимости задерживающего напряжения от частоты света (рис. 29) – один из наиболее точных методов определения величины .