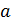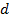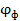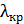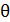План решения задач по теме «Интерференция света»
1. Прежде всего, необходимо на рисунке показать интерферирующие лучи и обозначить отрезки, определяющие геометрический путь этих лучей. Записывая оптическую разность хода, умножайте геометрический путь луча на показатель преломления той среды, в которой пройден путь.
2. Если интерферируют отраженные лучи, то следует указать соотношение показателей преломления 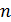 среды и отражающей пластинки (пленки). Это необходимо для того, чтобы учесть изменение фазы светового вектора при отражении от оптически более плотной среды (с большей величиной
среды и отражающей пластинки (пленки). Это необходимо для того, чтобы учесть изменение фазы светового вектора при отражении от оптически более плотной среды (с большей величиной 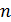 ) путем прибавления к оптической разности хода лучей слагаемого, равного
) путем прибавления к оптической разности хода лучей слагаемого, равного 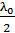 .
.
3. При использовании условий максимума интенсивности 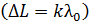 или минимума
или минимума 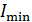
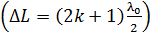 величину
величину 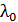 – длину волны света в вакууме можно с успехом заменить величиной
– длину волны света в вакууме можно с успехом заменить величиной 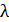 в воздухе, так как их отличие незначительно:
в воздухе, так как их отличие незначительно: 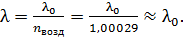
Задача 4. В опыте Юнга расстояние от щелей до экрана 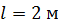 ; длина волны света
; длина волны света 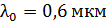 . Определите расстояние
. Определите расстояние 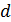 между щелями, если ширина интерференционной полосы
между щелями, если ширина интерференционной полосы 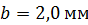 .
.
Дано 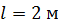 ; ; 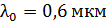 ; ; 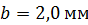 . . 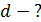 |
Решение
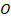 |
| · |
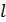 |
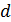 |
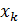 |
| экран |
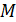 |
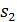 |
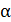 |
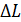 |
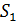 |
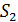 |
 |
 |
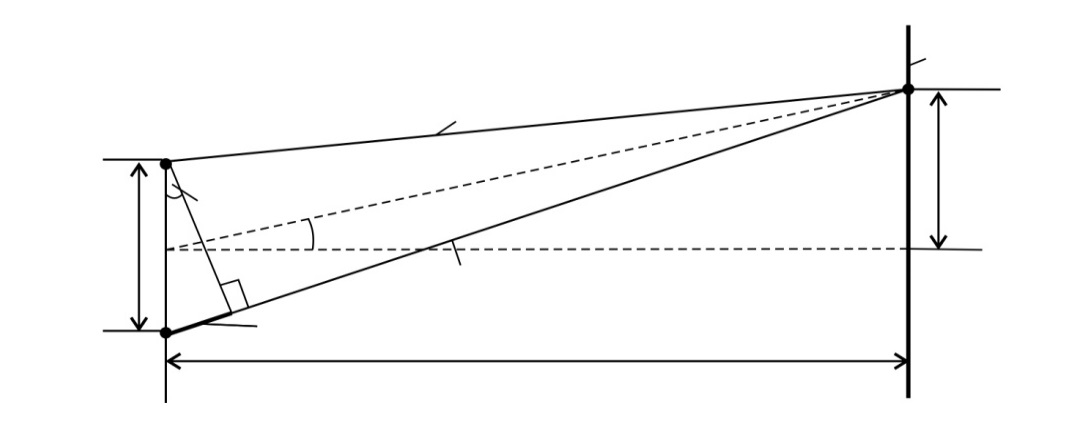
Рис. 31
В опыте Юнга интерферируют волны от двух щелей 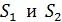 , расположенных на малом расстоянии
, расположенных на малом расстоянии 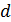 друг от друга (рис. 31). Эти щели являются когерентными источниками света, так как они находятся на одном фронте волны. Щели достаточно узкие и расположены перпендикулярно плоскости рисунка. Интерференционная картина на экране имеет вид полос, параллельных щелям. В центре картины (точка
друг от друга (рис. 31). Эти щели являются когерентными источниками света, так как они находятся на одном фронте волны. Щели достаточно узкие и расположены перпендикулярно плоскости рисунка. Интерференционная картина на экране имеет вид полос, параллельных щелям. В центре картины (точка 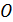 на рис. 31) будет светлая полоса (нулевой максимум), так как для этой точки оптическая разность хода лучей
на рис. 31) будет светлая полоса (нулевой максимум), так как для этой точки оптическая разность хода лучей 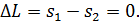
Пусть в точке 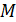 на экране будет -й интерференционный максимум, для которого оптическая разность хода волн от источников
на экране будет -й интерференционный максимум, для которого оптическая разность хода волн от источников 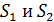 :
:
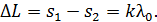 (1)
(1)
Для двух подобных треугольников (малого и большого на рис. 31), учитывая, что расстояние 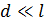 и угол
и угол 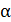 – весьма малый, запишем следующие соотношения:
– весьма малый, запишем следующие соотношения:
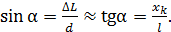 (2)
(2)
Здесь 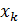 – расстояние от центрального (нулевого) максимума (в точке
– расстояние от центрального (нулевого) максимума (в точке 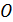 ) до -го максимума – в точке
) до -го максимума – в точке 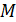 (см. рис. 31). Из соотношений (2) выразим величину
(см. рис. 31). Из соотношений (2) выразим величину 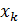 :
:
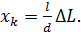 (3)
(3)
С учетом оптической разности хода волн, которая при показателе преломления воздуха 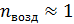 совпадает с разностью геометрических путей волн, записанной в формуле (1), равенство (3) принимает вид:
совпадает с разностью геометрических путей волн, записанной в формуле (1), равенство (3) принимает вид:
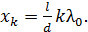 (4)
(4)
Для соседнего 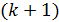 -го максимума запишем формулу, аналогичную (4):
-го максимума запишем формулу, аналогичную (4):
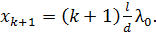 (4а)
(4а)
Используя формулы (4а) и (4), определим ширину интерференционной полосы как расстояние между двумя соседними максимумами:
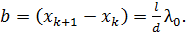 (5)
(5)
Из этой формулы получаем расчетную формулу расстояния 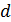 :
:
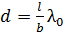 .
.
Вычисляем расстояние 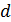 между щелями в опыте Юнга:
между щелями в опыте Юнга:
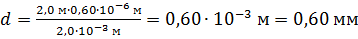 .
.
Задача 5. На тонкую пленку мыльной воды с показателем преломления 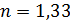 и толщиной
и толщиной 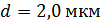 падает белый свет по нормали к поверхности пленки. Определите длины волн
падает белый свет по нормали к поверхности пленки. Определите длины волн 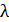 лучей видимого участка спектра (
лучей видимого участка спектра ( 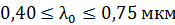 ), которые в отраженном свете будут усилены в результате интерференции.
), которые в отраженном свете будут усилены в результате интерференции.
Дано 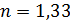 ; ; 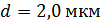 ; ; 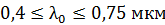 . . 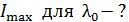 |
Решение
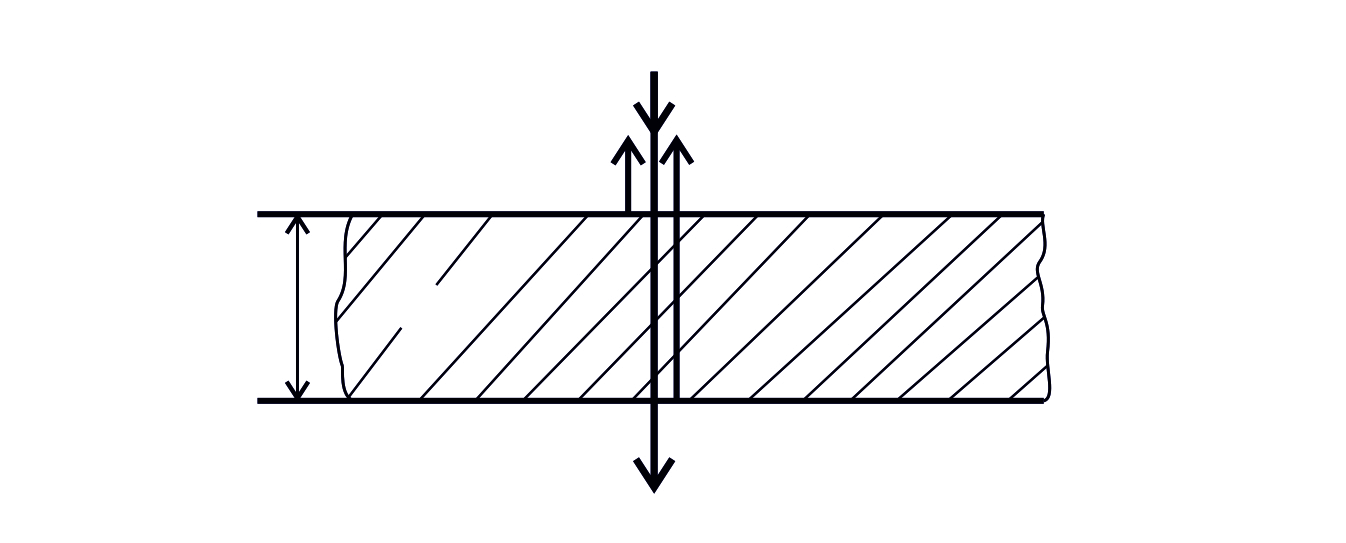
Рис. 32 |
В отраженном свете будут интерферировать два луча: 1-й, отраженный от верхней поверхности пленки, и 2-й, отраженный от нижней поверхности (рис. 32). Оптическая разность хода этих лучей:
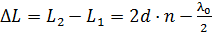 . (1)
. (1)
Дополнительное слагаемое, равное 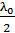 , обусловлено отражением 1-го луча от оптически более плотной пленки.
, обусловлено отражением 1-го луча от оптически более плотной пленки.
Условие максимумов интенсивности при интерференции волн:
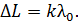 (2)
(2)
Приравняем величины 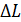 по формулам (1) и (2):
по формулам (1) и (2):
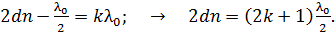 (3)
(3)
Из соотношения (3) выразим длины волн, удовлетворяющие условию 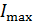 :
:
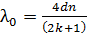 ; (4)
; (4)
Полагая в этой формуле величину 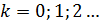 , вычислим длины волн
, вычислим длины волн 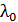 , усиленные в отраженном свете:
, усиленные в отраженном свете:
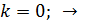
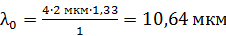 ; это инфракрасная область спектра.
; это инфракрасная область спектра.
Видимая область спектра начинается с номера максимума 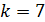 и соответствующие длины волн усиленных лучей, рассчитанные по формуле (4), будут следующие:
и соответствующие длины волн усиленных лучей, рассчитанные по формуле (4), будут следующие:
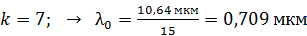 ; – красный цвет;
; – красный цвет;
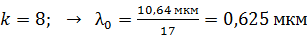 ; – желтый;
; – желтый;
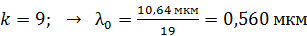 ; – зеленый;
; – зеленый;
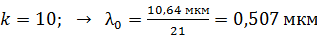 ; – голубой;
; – голубой;
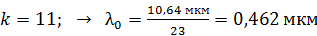 ; – синий;
; – синий;
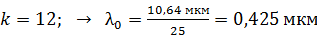 ; – фиолетовый;
; – фиолетовый;
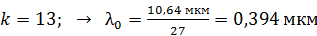 ; – фиолетовый;
; – фиолетовый;
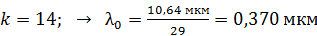 ; – начало ультрафиолетовой области спектра.
; – начало ультрафиолетовой области спектра.
Задача 6. На стеклянную линзу объектива с показателем преломления 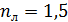 нанесена тонкая прозрачная пленка вещества с показателем преломления
нанесена тонкая прозрачная пленка вещества с показателем преломления 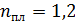 . Объектив освещен падающим на него нормально пучком света с длиной волны
. Объектив освещен падающим на него нормально пучком света с длиной волны 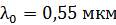 . Определите наименьшую толщину пленки
. Определите наименьшую толщину пленки 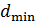 , при которой отраженный свет будет иметь минимальную интенсивность.
, при которой отраженный свет будет иметь минимальную интенсивность.
Дано 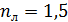 ; ; 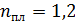 ; ; 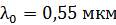 . . 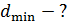 |
Решение
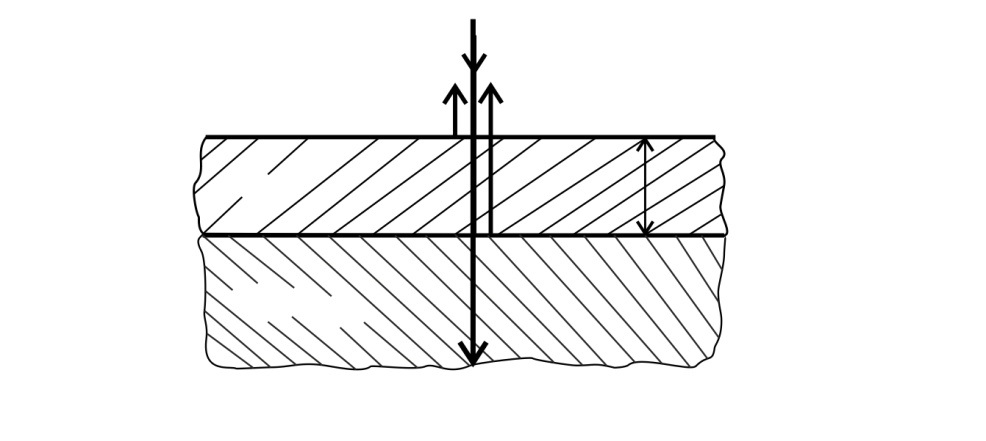
Рис. 33 |
В отраженном свете происходит интерференция лучей 1 и 2 (рис. 33), отраженных от пленки (луч 1) и от линзы (луч 2). Оптическая разность хода этих лучей определяется следующим образом:
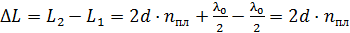 . (1)
. (1)
Здесь слагаемое, равное 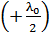 – при отражении 2-го луча, а слагаемое
– при отражении 2-го луча, а слагаемое 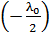 входит в вычитаемый оптический путь
входит в вычитаемый оптический путь 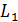 1-го луча, так как и тот, и другой луч отражается от оптически более плотной среды.
1-го луча, так как и тот, и другой луч отражается от оптически более плотной среды.
Чтобы отраженный луч имел наименьшую интенсивность, оптическая разность хода лучей 1 и 2 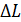 должна удовлетворять условию интерференционного минимума:
должна удовлетворять условию интерференционного минимума:
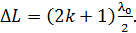 (2)
(2)
Приравниваем оптическую разность хода лучей по формулам (1) и (2): 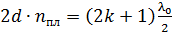 ;
; 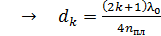 ; (3)
; (3)
Формула (3) дает дискретный набор толщин 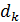 , соответствующих значениям
, соответствующих значениям 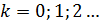 , при которых
, при которых 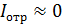 . Минимальное значение
. Минимальное значение 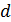 достигается при
достигается при 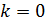 :
:
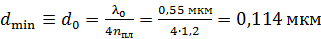 .
.
Отметим, что пленки толщиной 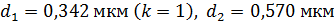 и др. также обеспечивают минимальную интенсивность отраженного света. При этом, согласно закона сохранения энергии,
и др. также обеспечивают минимальную интенсивность отраженного света. При этом, согласно закона сохранения энергии,
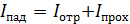 ,
,
интенсивность света, проходящего в объектив, – 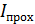 будет наибольшая, т. е. такая пленка просветляет область за объективом. Линзы с просветленной оптикой широко используются в оптических приборах.
будет наибольшая, т. е. такая пленка просветляет область за объективом. Линзы с просветленной оптикой широко используются в оптических приборах.
Задача 7. Между стеклянной пластинкой и лежащей на ней плосковыпуклой линзой с радиусом кривизны 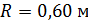 находится жидкость. При наблюдении в отраженном свете с длиной волны
находится жидкость. При наблюдении в отраженном свете с длиной волны 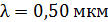 измерен радиус третьего темного кольца Ньютона:
измерен радиус третьего темного кольца Ньютона: 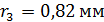 . Определите толщину слоя жидкости
. Определите толщину слоя жидкости 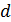 в том месте, где наблюдается это кольцо, и показатель преломления
в том месте, где наблюдается это кольцо, и показатель преломления 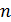 жидкости.
жидкости.
Дано 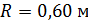 ; ; 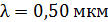 ; ; 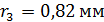 ; темное кольцо: ; темное кольцо: 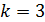 . . 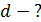 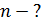 |
Решение
Рис. 34 |
В отраженном свете происходит интерференция лучей 1 и 2: 1-й отражается от жидкости, 2-й – от стекла (рис. 34). Предположим, что показатель преломления 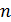 жидкости меньше, чем стеклянной пластинки и линзы
жидкости меньше, чем стеклянной пластинки и линзы 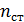 :
: 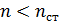 . В этом случае 2-й луч отражается от оптически более плотной среды с изменением фазы колебаний светового вектора на
. В этом случае 2-й луч отражается от оптически более плотной среды с изменением фазы колебаний светового вектора на 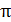 , что и учтем, прибавляя к оптической длине пути 2-го луча слагаемое
, что и учтем, прибавляя к оптической длине пути 2-го луча слагаемое 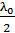 . Тогда оптическая разность хода лучей 1 и 2 представится формулой:
. Тогда оптическая разность хода лучей 1 и 2 представится формулой:
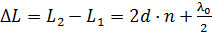 . (1)
. (1)
Радиус 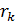 кольца Ньютона с номером
кольца Ньютона с номером 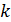 связан с параметрами установки (см. «Теоретическая часть», п. 2.1.2 г), формула (9)):
связан с параметрами установки (см. «Теоретическая часть», п. 2.1.2 г), формула (9)):
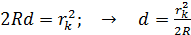 . (2)
. (2)
По этой формуле вычислим толщину слоя 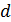 жидкости в том месте, где измерен радиус третьего кольца, подставляя
жидкости в том месте, где измерен радиус третьего кольца, подставляя 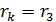 :
:
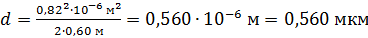 .
.
Чтобы найти показатель преломления 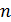 жидкости из формулы (1), учтем, что -е темное кольцо – это
жидкости из формулы (1), учтем, что -е темное кольцо – это 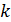 -й интерференционный минимум интенсивности, для которого оптическая разность хода лучей определяется условием минимума:
-й интерференционный минимум интенсивности, для которого оптическая разность хода лучей определяется условием минимума:
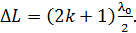 (3)
(3)
Приравнивая величину 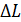 по формулам (1) и (3), получаем следующую расчетную формулу величины
по формулам (1) и (3), получаем следующую расчетную формулу величины 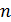 :
:
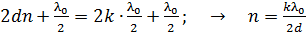 . (4)
. (4)
Вычисляем показатель преломления жидкости:
 .
.
Полученное значение 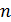 , с учетом погрешности измеренных величин
, с учетом погрешности измеренных величин 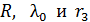 , совпадает с табличным значением показателя преломления воды
, совпадает с табличным значением показателя преломления воды 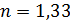 . Относительная погрешность
. Относительная погрешность 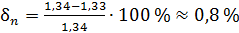 .
.
Задача 8. Между двумя плоскопараллельными пластинками на расстоянии 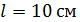 от линии их соприкосновения находится тонкая проволока диаметром
от линии их соприкосновения находится тонкая проволока диаметром 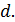 Пластинки, образующие воздушный клин, освещаются нормально падающим монохроматическим светом с длиной волны
Пластинки, образующие воздушный клин, освещаются нормально падающим монохроматическим светом с длиной волны 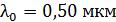 . Определите диаметр проволоки
. Определите диаметр проволоки 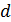 , если ширина интерференционных полос, наблюдаемых в отраженном свете,
, если ширина интерференционных полос, наблюдаемых в отраженном свете, 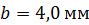 .
.
Дано 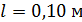 ; ; 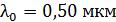 ; ; 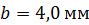 . . 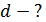 |
Решение
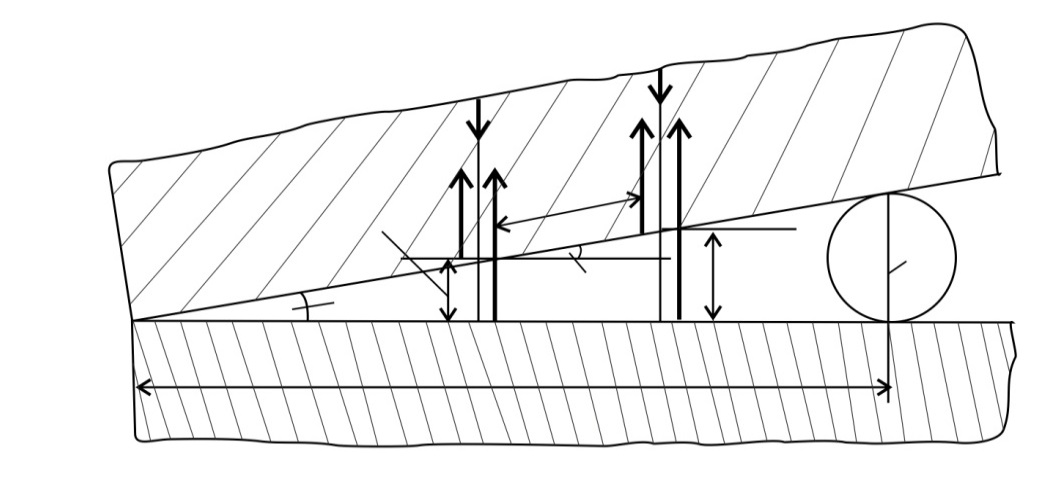
Рис. 35 |
На рис. 35 показаны две пары отраженных лучей: (1 и 2) и ( 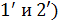 , при интерференции которых наблюдаются соседние полосы – с номером
, при интерференции которых наблюдаются соседние полосы – с номером 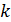 и (
и ( 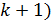 соответственно. Запишем оптическую разность хода лучей 1 и 2:
соответственно. Запишем оптическую разность хода лучей 1 и 2:
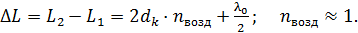 (1)
(1)
Пусть эти лучи при наложении дают темную полосу, т. е. величина 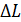 удовлетворяет условию интерференционного минимума:
удовлетворяет условию интерференционного минимума:
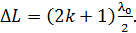 (2)
(2)
Приравнивая величину 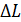 по формулам (1) и (2), выразим толщину слоя воздуха
по формулам (1) и (2), выразим толщину слоя воздуха 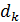 в том месте, где наблюдается -я темная полоса:
в том месте, где наблюдается -я темная полоса:
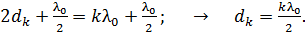 (3)
(3)
Аналогичную формуле (3) величину 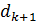 получим для соседней (
получим для соседней ( 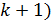 -й темной полосы:
-й темной полосы:
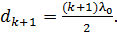 (4)
(4)
Чтобы найти искомую величину диаметра проволоки 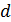 , на рисунке рассмотрим два подобных прямоугольных треугольника: малый – со сторонами
, на рисунке рассмотрим два подобных прямоугольных треугольника: малый – со сторонами 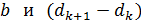 и большой – со сторонами
и большой – со сторонами 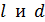 . Для малого угла
. Для малого угла 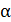 (он мал, так как
(он мал, так как 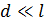 ) в этих треугольниках выполняется следующее равенство:
) в этих треугольниках выполняется следующее равенство:
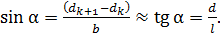 (5)
(5)
Здесь, в соответствии с полученными выше формулами (3) и (4), разность величин 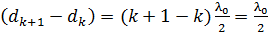 . Учитывая это, из выражения (5) получаем следующую расчетную формулу:
. Учитывая это, из выражения (5) получаем следующую расчетную формулу:
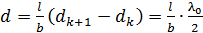 . (6)
. (6)
Вычисляем диаметр проволоки 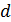 :
:
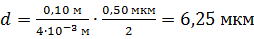 .
.
Таким образом, интерференционную картину полос равной толщины воздушного клина можно использовать для точного определения размеров малых тел.
3.2. План решения задач по теме «Дифракция света»
1. Условия дифракционных максимумов и минимумов различны для дифракции на щели, плоской дифракционной решетке и на кристалле – пространственной дифракционной решетке. Поэтому, согласно условию задачи, нужно выбрать соответствующие формулы (см. «Теоретическая часть», п. 2.2).
2. На рисунке, сопровождающем решение задачи, следует показать угол дифракции 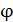 . В решении задачи для малых углов
. В решении задачи для малых углов 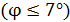 можно использовать формулу приближенных вычислений:
можно использовать формулу приближенных вычислений: 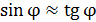 . В случае больших углов дифракции следует использовать тригонометрическое соотношение
. В случае больших углов дифракции следует использовать тригонометрическое соотношение 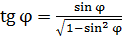 .
.
Задача 9. На диафрагму со щелью шириной 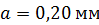 падает нормально плоская монохроматическая волна с длиной волны
падает нормально плоская монохроматическая волна с длиной волны 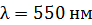 . Определите ширину изображения
. Определите ширину изображения 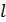 щели на экране как расстояние между первыми дифракционными минимумами. Экран расположен параллельно плоскости диафрагмы на расстоянии
щели на экране как расстояние между первыми дифракционными минимумами. Экран расположен параллельно плоскости диафрагмы на расстоянии 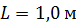 от нее. Дифракционная картина проецируется на экран линзой, расположенной близко к щели.
от нее. Дифракционная картина проецируется на экран линзой, расположенной близко к щели.
Решение
Дано 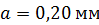 ; ; 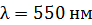 ; ; 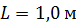 . . 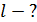 |
Рис. 36 |
Дифракционный спектр от щели – график распределения интенсивности света вдоль экрана 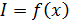 , – показан на рис. 36. Расчет интенсивностей дифракционных максимумов показывает, что интенсивности 1-го, 2-го, 3-го и последующих максимумов малы по сравнению с
, – показан на рис. 36. Расчет интенсивностей дифракционных максимумов показывает, что интенсивности 1-го, 2-го, 3-го и последующих максимумов малы по сравнению с 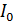 – высотой нулевого максимума:
– высотой нулевого максимума: 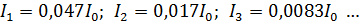 . Таким образом, основная часть энергии приходится на центральный (нулевой) максимум; поэтому его ширина
. Таким образом, основная часть энергии приходится на центральный (нулевой) максимум; поэтому его ширина 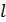 и является изображением щели на экране.
и является изображением щели на экране.
Ширина центрального максимума ограничивается примыкающими к нему дифракционными минимумами первого порядка: 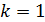 . Условие этих минимумов: размещение на открытом щелью фронте волны 2-х зон Френеля, – при этом оптическая разность хода
. Условие этих минимумов: размещение на открытом щелью фронте волны 2-х зон Френеля, – при этом оптическая разность хода 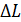 крайних лучей, идущих от щели под углом дифракции
крайних лучей, идущих от щели под углом дифракции 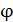 , равна четному числу полуволн
, равна четному числу полуволн  :
:
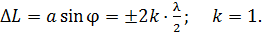 (1)
(1)
Из этого условия получаем, что для углов дифракции 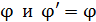 синус угла:
синус угла:
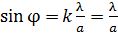 . (2)
. (2)
Параллельные интерферирующие лучи, идущие от щели под углами 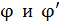 , собираются линзой в точках
, собираются линзой в точках 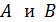 соответственно (см. рис 36). Из треугольника на рисунке видно, что полуширина
соответственно (см. рис 36). Из треугольника на рисунке видно, что полуширина  искомого изображения щели на экране определяется через тангенс угла дифракции:
искомого изображения щели на экране определяется через тангенс угла дифракции:
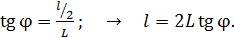 (3)
(3)
Учитывая, что для малых углов 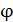 значение
значение 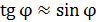 и используя условие (2), получаем следующую расчетную формулу величины
и используя условие (2), получаем следующую расчетную формулу величины 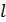 :
:
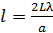 . (4)
. (4)
Вычисляем ширину изображения щели на экране как ширину центрального дифракционного максимума:
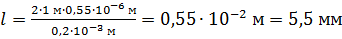 .
.
Проверим использованное в решении условие малости угла 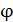 : определим этот угол по формуле (3):
: определим этот угол по формуле (3):
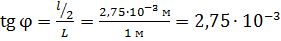 .
. 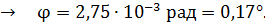
Задача 10. На дифракционную решетку (ДР), содержащую 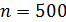 штрихов на одном миллиметре длины, падает нормально белый свет. Линзой, помещенной вблизи решетки, дифракционный спектр проецируется на экран. Определите длину
штрихов на одном миллиметре длины, падает нормально белый свет. Линзой, помещенной вблизи решетки, дифракционный спектр проецируется на экран. Определите длину 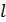 спектра второго порядка на экране, если расстояние от линзы до экрана
спектра второго порядка на экране, если расстояние от линзы до экрана 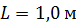 . Длины волн границ видимого спектра:
. Длины волн границ видимого спектра: 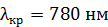 ,
, 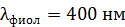 .
.
Дано 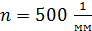 ; ; 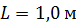 ; ; 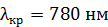 ; ; 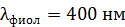 ; ; 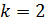 . . 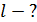 |
Решение
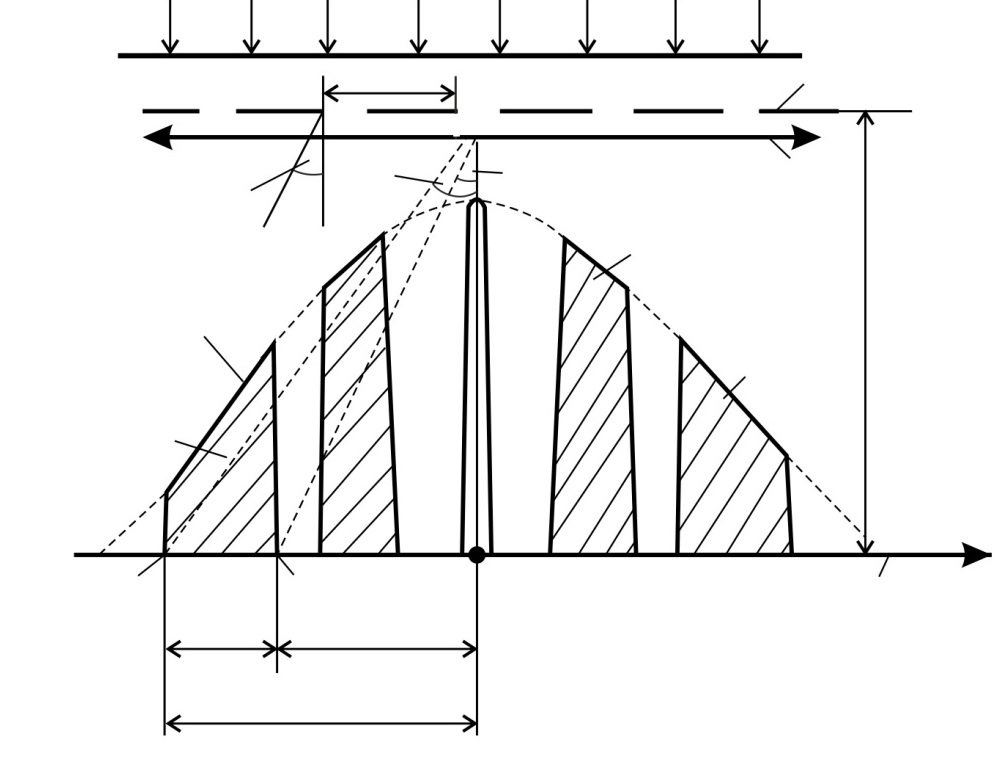
Рис. 37 |
Дифракционный спектр от решетки – график распределения интенсивности света 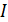 вдоль экрана:
вдоль экрана: 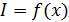 , – показан на рис. 37. Запишем условие главных максимумов в спектре дифракционной решетки для границ белого света – фиолетового и красного лучей:
, – показан на рис. 37. Запишем условие главных максимумов в спектре дифракционной решетки для границ белого света – фиолетового и красного лучей:
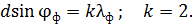 (1)
(1)
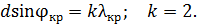 (2)
(2)
Здесь период дифракционной решетки 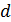 связан с числом щелей на 1 мм решетки очевидным соотношением:
связан с числом щелей на 1 мм решетки очевидным соотношением:
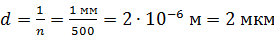 .
.
Так как длина волны красного света 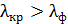 , то, согласно уравнениям (1) и (2), угол дифракции
, то, согласно уравнениям (1) и (2), угол дифракции 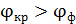 . Соответственно, красная линия в спектре ДР отстоит от центрального максимума (точка
. Соответственно, красная линия в спектре ДР отстоит от центрального максимума (точка 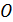 на рис. 37) на расстояние
на рис. 37) на расстояние 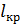 , а фиолетовая линия – на
, а фиолетовая линия – на 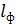 ; причем
; причем 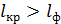 (см. рис. 37). Как видно по графику спектра, длина
(см. рис. 37). Как видно по графику спектра, длина 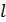 спектра второго порядка равна разности этих расстояний:
спектра второго порядка равна разности этих расстояний:
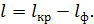 (3)
(3)
Каждое из этих расстояний определяется углом дифракции 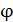 и расстоянием
и расстоянием 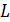 от решетки до экрана (линза установлена вблизи дифракционной решетки); как следует из треугольников на рисунке:
от решетки до экрана (линза установлена вблизи дифракционной решетки); как следует из треугольников на рисунке:
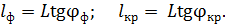 (4)
(4)
Расчетная формула (3) длины спектра 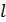 , с учетом формул (4), принимает следующий вид:
, с учетом формул (4), принимает следующий вид:
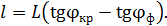 (5)
(5)
Определим углы дифракции для спектра 2-го порядка ( 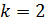 ) из условий максимумов (2) и (1):
) из условий максимумов (2) и (1):
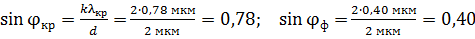 .
.
Значения, синусов углов дифракции существенно больше нуля, следовательно, углы дифракции не являются малыми; поэтому определим величину 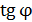 по известному тригонометрическому соотношению:
по известному тригонометрическому соотношению:
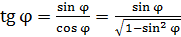 ;
; 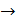
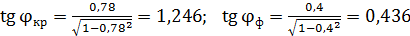 .
.
Используя эти значения тангенсов углов дифракции, вычисляем по формуле (5) длину спектра 2-го порядка при дифракции белого света на данной дифракционной решетке:
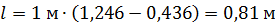 .
.
Задача 11. На дифракционную решетку (ДР), постоянная которой 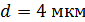 , падает нормально свет с длиной волны
, падает нормально свет с длиной волны 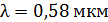 . Определите наибольший порядок максимума
. Определите наибольший порядок максимума 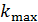 , который дает эта решетка, угол дифракции
, который дает эта решетка, угол дифракции 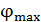 для этого максимума и общее число максимумов
для этого максимума и общее число максимумов 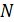 .
.
Дано 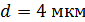 ; ; 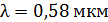 . . 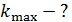 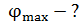 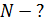 |
Решение
 |
 |
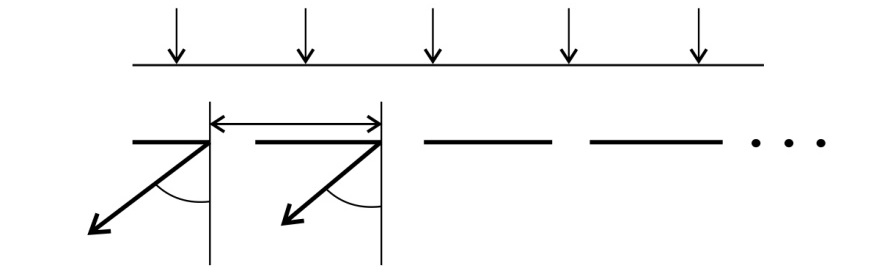
Рис. 38
Запишем условие главных максимумов для дифракционной решетки:
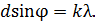 (1)
(1)
Из равенства (1) выразим порядок максимума 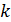 :
:
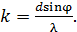 (2)
(2)
Формула (2) показывает, что наибольший порядок спектра 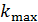 при заданных значениях
при заданных значениях 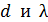 соответствует максимальному значению
соответствует максимальному значению 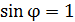 . Вычисляем величину
. Вычисляем величину 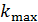 по формуле (2):
по формуле (2):
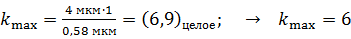 .
.
Взята целая часть найденного числа, так как порядок максимума 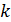 – целое число; Округление до 7 недопустимо, поскольку
– целое число; Округление до 7 недопустимо, поскольку 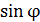 не может быть больше единицы.
не может быть больше единицы.
Значение угла дифракции 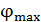 (рис. 38) для максимума 6-го порядка определим по условию главных максимумов (1):
(рис. 38) для максимума 6-го порядка определим по условию главных максимумов (1):
 .
.
Общее число максимумов в спектре ДР определим следующим образом. По графику дифракционного спектра решетки (см. «Теоретическая часть», рис. 16 а) видно, что в спектре есть центральный (нулевой: 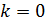 ) максимум, а слева и справа от него располагаются максимумы с номерами
) максимум, а слева и справа от него располагаются максимумы с номерами 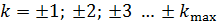 . Суммируя число всех максимумов, определяем величину
. Суммируя число всех максимумов, определяем величину 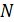 :
:
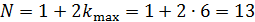 .
.
Задача 12. Дифракционная решетка (ДР) длиной 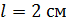 позволяет разрешить в спектре первого порядка две спектральные линии калия:
позволяет разрешить в спектре первого порядка две спектральные линии калия: 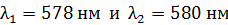 . Определите общее число щелей
. Определите общее число щелей 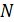 этой ДР и ее постоянную
этой ДР и ее постоянную 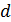 .
.
Дано 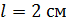 ; ; 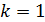 ; ; 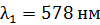 ; ; 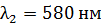 . . 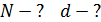 |
Данные спектральные линии с длинами волн 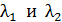 разрешаются данной дифракционной решеткой (см. «Теоретическая часть», рис. 17 а), следовательно, ее разрешающая способность определяется формулой: разрешаются данной дифракционной решеткой (см. «Теоретическая часть», рис. 17 а), следовательно, ее разрешающая способность определяется формулой: 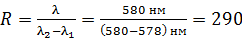 . (1) Величина разрешающей способности . (1) Величина разрешающей способности 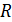 зависит от общего числа щелей зависит от общего числа щелей 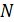 дифракционной решетки следующим образом: дифракционной решетки следующим образом: |
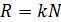 , (2)
, (2)
где 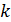 – порядок спектра, в котором разрешены линии.
– порядок спектра, в котором разрешены линии.
Выразим из формулы (2) число щелей 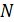 дифракционной решетки и вычислим величину
дифракционной решетки и вычислим величину 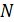 , полагая, по условию задачи,
, полагая, по условию задачи, 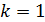 :
:
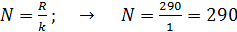 .
.
Период дифракционной решетки 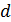 повторяется
повторяется 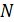 раз на длине решетки
раз на длине решетки 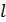 , что позволяет записать очевидное соотношение этих величин:
, что позволяет записать очевидное соотношение этих величин:
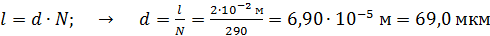 .
.
Задача 13. На грань кристалла под углом 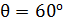 к ней падает параллельный пучок рентгеновского излучения с длиной волны
к ней падает параллельный пучок рентгеновского излучения с длиной волны 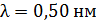 . Определите расстояние
. Определите расстояние 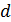 между атомными плоскостями кристалла, при отражении от которых наблюдается дифракционный максимум первого порядка.
между атомными плоскостями кристалла, при отражении от которых наблюдается дифракционный максимум первого порядка.
Дано 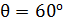 ; ; 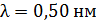 ; ; 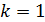 ; ; 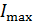 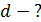 |
Рис. 39 |
Условие дифракционных максимумов при дифракции рентгеновского излучения на кристалле – это формула Вульфа – Брэггов:
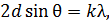 (1)
(1)
где 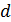 – расстояние между атомными плоскостями, отражающими рентгеновские лучи (рис. 39).
– расстояние между атомными плоскостями, отражающими рентгеновские лучи (рис. 39).
Определим из формулы (1) величину 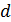 и вычислим ее:
и вычислим ее:
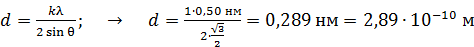 .
.
План решения задач по теме «Поляризация света»
1. Выясните, какое явление: поляризация света при отражении, прохождение света через поляроиды, двойное лучепреломление или поворот плоскости поляризации света оптически активным веществом, – рассматривается в данной задаче. Изучите описание явления по разделу «Теоретическая часть».
2. При решении задач, связанных с поляризацией света при отражении от диэлектриков с использованием закона Брюстера: 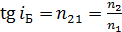 , – следует иметь в виду, что нумерация сред – 1-я и 2-я (индекс их показателей преломления
, – следует иметь в виду, что нумерация сред – 1-я и 2-я (индекс их показателей преломления 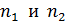 ) выполняется по ходу луча.
) выполняется по ходу луча.
Задача 14. Параллельный луч света переходит из воды в стекло; при этом луч, отраженный от границы раздела этих сред, оказывается максимально поляризованным. Определите угол 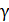 между падающим и преломленным лучами.
между падающим и преломленным лучами.
Дано 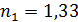 ; ; 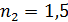 ; ; 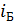 . . 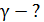 |
Решение
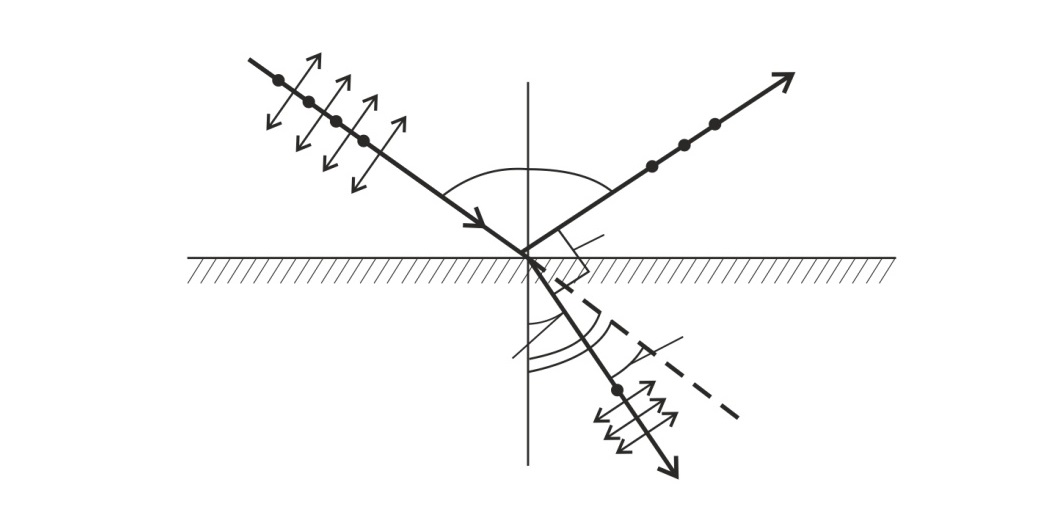
Рис. 40 |
Так как по условию задачи отраженный от стекла луч полностью поляризован, то угол падения луча на границу раздела сред равен углу Брюстера 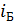 , удовлетворяющему закону Брюстера:
, удовлетворяющему закону Брюстера:
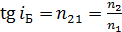 . (1)
. (1)
Определим угол Брюстера:
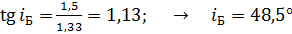 .
.
По рис. 40, на котором падающий луч продолжен во 2-ю среду – в стекло, видно, что угол 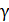 между падающим и преломленным лучом определяется соотношением:
между падающим и преломленным лучом определяется соотношением:
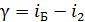 , (2)
, (2)
где 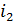 – угол преломления луча.
– угол преломления луча.
Определим угол преломления 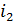 по закону преломления света:
по закону преломления света:
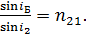 (3)
(3)
Сравнивая формулы законов (3) и (1), получаем следующие соотношения:
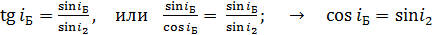 . (4)
. (4)
Из формулы (4) следует, что углы 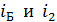 – дополнительные:
– дополнительные:
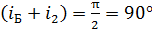 . (5)
. (5)
По рис. 40 видно, что сумма углов 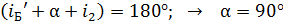 , т. е. при падении света под угл
, т. е. при падении света под угл
Дата добавления: 2016-10-07; просмотров: 4905;

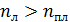
 ;
;