Неравенство Чебышева.

Предмет теории вероятностей, как мы знаем (см. §1. гл.I), составляют закономерности, свойственнее массовым случайным событиям. Простейшая из них - устойчивость относительной частоты – лежит в основе всех приложений теории вероятностей к практике. Общий смысл подобных закономерностей сводится к следующему. Пусть производится большая серия однотипных опытов. Исход каждого отдельного опыта является случайным, неопределённым. Однако, несмотря на это, средний результат всей серии опытов утрачивает случайный характер, становится закономерным. Под законом больших чисел в теории вероятностей понимается ряд теорем, в каждой из которых устанавливается факт приближения средних характеристик большого числа опытов к некоторым определённым постоянным.

В основе доказательства этих теорем лежит важное неравенство, установленное в 1845г. П.Л. Чебышевым.

Неравенство Чебышева. Пусть имеется случайная величина 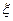с математическим ожиданием Mξ=m и дисперсией Dξ=D. Каково бы ни было положительное число ε, вероятность того, что величина ξ отклонится от своего математического ожидания не меньше чем на ε, ограничена с верху числом 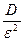, то есть

P(|ξ –m|≥ ε )≤ 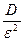. (1)

Замечание. Поясним смысл неравенства Чебышева. Выберем некоторое положительное число 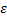и рассмотрим событие

( |ξ –m|≥ ε ) . (2)

Геометрически смысл этого события заключается в том, что значение случайной величины попадает в область числовой оси, получающейся удалением из всей оси интервала (m-ε;m+ε) (см. рис.1).

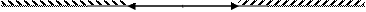
С возрастанием 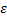эта область сужается, следовательно, вероятность попадания в неё (т.е. вероятность события (2)) становится меньше. Неравенство Чебышева устанавливает для этой вероятности весьма простую оценку, а именно: вероятность такого «слишком большого» отклонения от среднего может быть оценена через дисперсию Dξ и число ε.

Если фиксировать ε, то вероятность непопадания в интервал (m-ε, m+ε) тем меньше, чем меньше дисперсия Dξ. Это вполне соответствует истолкованию дисперсии, как «меры разброса» случайной величины. Заметим ещё, что для противоположного события к событию ( |ξ –m|≥ ε ) имеем:

P( |ξ –m|<ε )=1 – P( |ξ–m|≥ε ) ≥ 1- 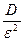. (3)

Доказательство неравенства Чебышева.Рассмотрим отдельно случай дискретной и непрерывной случайной величины ξ.

Неравенство (1) является следствием другого неравенства, так же принадлежащего Чебышеву:

пусть случайная величина η принимает только неотрицательные значения (т.е. P(η <0)=0), тогда

P(η ≥1) 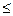Mη .(4)

Докажем сначала неравенство (4). Пусть η - дискретная случайная величина, принимающая неотрицательные значения x₁, x₂,..., с вероятностями p₁, p₂,… соответственно. Имеем

P(η ≥1) .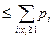

Если каждое слагаемое p_i cуммы, стоящей справа, умножить на соответствующее значение x_i то правая часть не уменьшится, поскольку x_i ≥1. Тогда получаем

P(η ≥1) .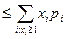

Выражение, стоящее справа, опять-таки не уменьшится, если распространить суммирование на все возможные значения η: действительно, при этом добавится неотрицательные слагаемые 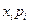, отвечающие таким номерам i, для которых x_i <1. Тогда получаем

P(η ≥1) .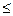

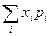Последняя сумма по определению совпадает Mη. Тем самым неравенство (4) доказано для случая ДСВ η.

Пусть, теперь, η - непрерывная случайная величина с плотностью p_η(x)= p (x). Пусть p(x) непрерывна функция, тогда, поскольку

p (η <0)= ,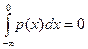

то отсюда следует, что p (x)=0 при x<0 .

Рассуждая аналогично, как и в дискретном случае, получаем

.

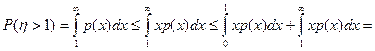
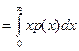Поскольку p(x)=0 при x<0, продолжая, получим

P(η >1) .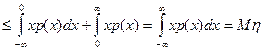

Тем самым неравенство (4) доказано для случая НСВ η.

Докажем теперь неравенство (1). Событие ( |ξ–m|>ε ) равносильно событию ( 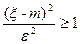). Случайная величина 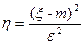принимает лишь неотрицательные значения, и к ней можно применить неравенство (4). Получим:

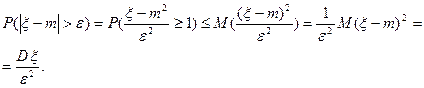В конечном итоге получаем: P( |ξ–m|>ε )≤ .

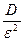Тем самым неравенство Чебышева доказано.

Пример. Оценим вероятность события (|ξ–m|<3σ), где σ– среднее квадратичное отклонение величины ξ .

Решение. Полагая в (3) ε=3σ, получим

P .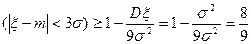

Таким образом, вероятность события (m-3σ<ξ<m+3σ) не меньше .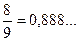

В действительности, для подавляющего большинства, встречающихся на практике случайных величин, эта вероятность значительно ближе к единице, чем .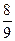

Например, для нормального распределения (см §3 гл.II) Она равна 0,997… .

Обычно, если закон распределения случайной величины неизвестен, но указаны параметры m=Mξ, и σ принимают, что диапазон практически возможных значений случайной величины есть интервал (m-3σ,m+3σ) («правило трех сигм»).