Закон больших чисел.

Неравенство Чебышева позволяет доказать ряд теорем, объединённых общим названием, «закон больших чисел». Основная из этих теорем принадлежит самому Чебышеву.

Теорема Чебышева. Пусть ξ₁,ξ₂…- последовательность независимых случайных величин, имеющих конечные дисперсии, ограниченные одной и той же постоянной и одно и тоже математическое ожидание (среднее значении):

Mξ₁=Mξ₂=…=m, Dξ₁<c, Dξ₂<c, … .

Тогда, каково бы ни было положительное число 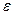>0, вероятность события

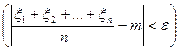
стремится к единице при n→ 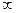, т.е.

.

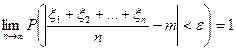Доказательство. Положим

.

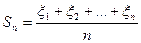В силу свойств математического ожидания имеем:

.

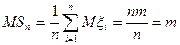Далее, так как величины ξ₁,ξ_2.,… ξ_n независимы, то

.

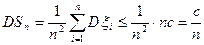Применим теперь к случайной величине η неравенство Чебышева:

P(|S_n–M S_n |<ε)>1-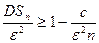

или

1 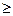P(|S_n–m|<ε) 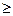1- .

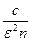Правая часть неравенства стремится к 1 при n 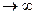; тем более стремится к 1 левая часть, а это и требовалось доказать.

Поясним содержание теоремы Чебышева на важном примере.

Пусть требуется измерить значение m некоторой физической величины. В силу неизбежных при измерении ошибок результат измерения будет случайной величиной ξ. Её математическое ожидание будет совпадать с измеряемой величиной m, а дисперсия равна некоторой величине D (характеризующей точность измерительного прибора). Произведём n измерений в одинаковых условиях, что обеспечивает независимость результатов. Результат к-го измерения есть некоторое случайное число x^(k), этим задана случайная величина ξ_k . Совокупность величин ξ₁,…,ξ_n представляет собой систему n независимых случайных величин, каждая из которых имеет тот же закон распределения, что и сама величина ξ. После серии из n измерений составим среднее арифметическое из n наблюдаемых значений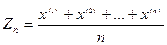

то есть значение случайной величины.

.

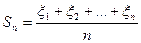Теорема Чебышева утверждает, что экспериментальное среднее Z_n «почти достоверно» оказывается близким к теоретическому среднему значению m (истинное значение физической величины) искомой физической величины, если только число испытаний n достаточно велико.

Тем самым оправдывается рекомендуемый в практической деятельности способ получения более точных результатов измерений: одна и та же величина измеряется многократно, и в качестве её значения берётся среднее арифметическое полученных результатов измерений.

Замечание. Близость к Mξ среднего арифметического опытных значений величины ξ уже нами показывалось при введении понятия математического ожидания. Однако соответствующее рассуждение относилось только к дискретным величинам; кроме того, высказывание о близости мотивировалось соображениями эмпирического характера. В противоположность этому теорема Чебышева даёт точную характеристику близости среднего арифметического к Mξ, и при том для любой случайной величины (строго доказывается, исходя из аксиом теории вероятностей).

Из теоремы Чебышева в качестве следствия можно получить другую важную теорему, которая впервые была доказана Я. Бернулли и опубликована в 1713 году.

Теорема Бернулли. Пусть производится n независимых опытов, в каждом из которых с вероятностью p может наступить некоторое событие А. Рассмотрим случайную величину 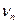– число наступления события А в n опытах. Тогда, каково бы ни было положительное число ε > 0, вероятность события

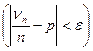
стремится к единицe при n→ 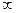, т.е.

.

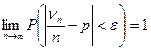Иначе говоря, как бы ни было мало ε, с увеличением числа опытов становится сколь угодно достоверным тот факт, что частота наступления события А отличается от вероятности этого события меньше, чем на ε.

Доказательство. Выведем теорему Бернулли из теоремы Чебышева. Заметим (см. § 7 гл. II), что

,

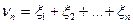где 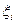есть число наступлений события А в i-м опыте (i=1,2,..,n).

Случайные величины 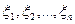имеют один и тот же закон распределения:

Значение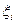
Вероятности	q	p

где 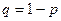. Для каждой из них математическое ожидание равно p, а дисперсия pq. Таким образом, все условия теоремы Чебышева выполняются, и для среднего арифметического величин 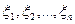, т.е. для 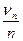справедливо соотношение

.

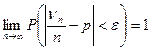Тем самым мы доказали теорему Бернулли.

Замечание. Отметим попутно следующий полезный факт.

Поскольку

,

,

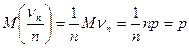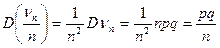то неравенство Чебышева, применительно к случайной величине 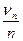, даёт:

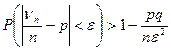. (1)

Мы получаем оценку ( хотя и весьма грубую) для вероятности отклонения частоты события А в серии из n опытов от вероятности события А в одном опыте.

Опытная проверка закона больших чисел предпринималась неоднократно. В приведённой ниже таблице приведены результаты опытов бросания монеты (событие А-выпадение герба, ) :

Экспериментатор	Число n бросаний	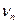-число выпадений герба	Частота выпадения герба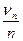
Ж.Бюффон (XVIII.) К. Пирсон К. Пирсон			0,507 0,5016 0,5005