Уравнение Бернулли для потока вязкой жидкости

Для получения уравнения Бернулли необходимо просуммировать энергию всех элементарных струек жидкости и потери энергии при её движении.

Обозначим через Э₁ и Э₂ полные энергии потока в двух произвольно взятых сечениях 1-1 и 2-2. Тогда баланс энергий для взятой жидкости выразится уравнением:

Э₁=Э₂+ 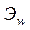, (3.30)

где 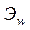– полная энергия, потерянная жидкостью при движении на рассматриваемом участке.

Запишем баланс средних удельных энергий потока. Для этого поделим уравнение (3.30) на весовой расход потока 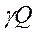. Получим:

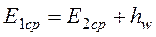, (3.31)

где 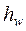– средняя потеря удельной энергии потока жидкости между сечениями 1-1 и 2-2, равная

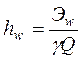. (3.32)

Данная зависимость является уравнением Бернулли для потока вязкой жидкости в первичном виде. Для получения уравнения в развёрнутом виде необходимо раскрыть выражения средних удельных энергий, каждое из которых сложится из средней потенциальной 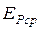и средней кинетической 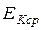энергии потока.

Поскольку для параллельно-струйных потоков величина удельной потенциальной энергии является постоянной во всех точках поперечного сечения потока жидкости, то средняя потенциальная энергия в каком-либо сечении может быть определена как сумма удельной энергии давления и удельной энергии положения, т.е.:

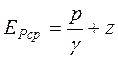. (3.33)

Для определения среднего значения удельной кинетической энергии сначала найдём кинетическую энергию для всего потока жидкости в данном сечении. Полную кинетическую энергию найдём интегрированием энергий по всем элементарным струйкам в пределах данного сечения, перед этим умножим удельную кинетическую энергию струйки на элементарный весовой расход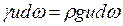

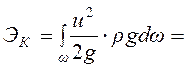
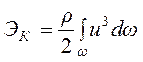. (3.34)

Поскольку распределение скорости по живому сечению определить довольно сложно, найдём кинетическую энергию потока через условную кинетическую энергию 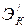, вычисляемую по средней скорости

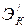
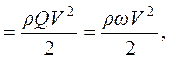(3.35)

где 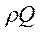- расход потока по массе жидкости.

Кинетическая энергия, подсчитанная по средней скорости, всегда меньше фактической кинетической энергии.

Отношение действительной кинетической энергии к кинетической энергии, подсчитанной по средней скорости обозначим через .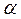

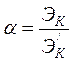. (3.36)

Тогда фактическая кинетическая энергия выразится зависимостью:

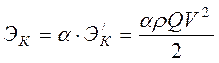. (3.37)

Поделив кинетическую энергию на весовой расход потока, найдём среднюю кинетическую энергию потока

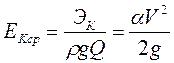. (3.38)

Тогда средняя удельная энергия потока в каком-либо сечении будет равна:

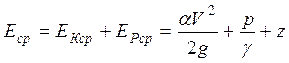. (3.39)

Подставляя (3.39) в уравнение (3.31), окончательно получим уравнение Бернулли для потока вязкой жидкости

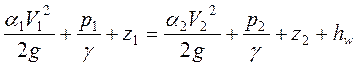, (3.40)

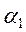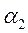где и - коэффициенты кинетической энергии (Кориолиса), выражающие отношение действительной кинетической энергии потока к кинетической энергии, вычисленной в предположении, что скорости во всех точках живого сечения равны средней скорости потока (или характеризующие неравномерность распределения скоростей в соответствующих поперечных сечениях потока).

При практическом применении уравнения Бернулли (3.40) следует иметь в виду, что оно приемлемо только для параллельно-струйных потоков и потоков с плавно изменяющимся движением жидкости. Значения геометрических высот и давлений, входящих в это уравнение для напорных потоков принято брать по точкам, лежащим на оси потока.

Значения поправочных коэффициентов 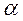в общем случае могут изменяться в пределах от 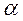= 1, для абсолютно невязких жидкостей до 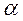= 2, для потоков, движущихся в ламинарном режиме. В практических расчётах при турбулентном режиме движения жидкости обычно принимают 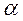=1.05 … 1.10 . В тех случаях, когда величина 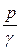>> 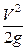без особых потерь точности можно принимать 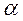=1.