Уравнение Бернулли для элементарной струйки вязкой жидкости

При движении вязкой жидкости вдоль твёрдой стенки происходит торможение потока вследствие влияния его вязкости и действия сил молекулярного сцепления между жидкостью и твёрдой стенкой. Поэтому наибольшей величины скорость достигает в центральной части потока, а по мере приближения к стенке скорость уменьшается практически до нуля (рис. 3.6).

При таком движении по поверхности со- Рис.3.6

прикосновения элементарных струек, движущихся с различными скоростями, возникают силы внутреннего трения, препятствующие движению жидкости. Поэтому вязкая жидкость будет затрачивать часть своей энергии на преодоление сил внутреннего трения, возникающих при относительном перемещении элементарных струек. Рассмотрим движение элементарной струйки вязкой жидкости (рис.3.7).

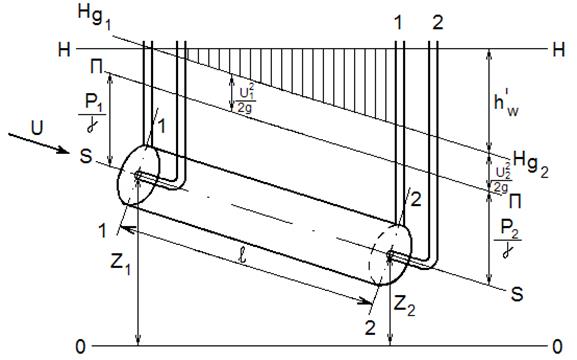
Рис. 3.7

1 – пьезометр; 2 – скоростная трубка (трубка Пито); П-П – пьезометрическая линия; Н-Н – напорная линия; Hg₁-Hg₂ – линия гидродинамического напора; О-О – плоскость сравнения;

Пьезометр измеряет пьезометрический напор, который является мерой потенциальной энергии жидкости, он равен:

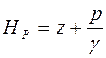. (3.25)

Движущаяся жидкость, кроме потенциальной энергии обладает ещё и кинетической. Удельную кинетическую энергию можно измерить, если в данной точке жидкость остановить. Тогда кинетическая энергия перейдёт в потенциальную и может быть измерена пьезометром. С этой целью в данной точке одновременно с пьезометром устанавливается трубка Пито. В ней жидкость поднимается на некоторую высоту, большую, чем в пьезометрической трубке, соответствующую удельной кинетической энергии, т.е. u²/2g.

Мы ранее отмечали, что часть энергии вязкой жидкости будет затрачена на преодоление сил внутреннего трения между струйками. Она перейдёт в тепловую энергию, и для жидкости будет безвозвратно теряться.

В результате этого, величина удельной энергии жидкости в сечении 2-2 окажется меньше величины удельной энергии в сечении 1-1, т.е. Е₁ >Е₂.

Значит, на участке движения жидкости от сечения 1-1 до сечения 2-2 потеря удельной энергии составляет величину:

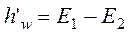. (3.26)

Перепишем в следующем виде:

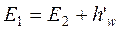. (3.27)

Поскольку полная удельная энергия движущейся жидкости равна гидродинамическому (полному) напору в данном сечении, то запишем:

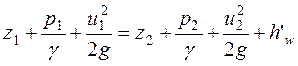. (3.28)

Это есть уравнение Бернулли для элементарной струйки вязкой жидкости.

Геометрически удельные энергии в сечениях 1-1 и 2-2 представлены на рис.3.7 гидродинамическими напорами Hg₁ и Hg₂ .

Гидродинамические напоры определяются геометрической суммой высот: геометрической, пьезометрической, скоростной.

Так как движение вязкой жидкости происходит с уменьшением её энергии, то и гидродинамические напоры по мере движения будут постепенно убывать. Потеря энергии на участке движения жидкости будет равна разности гидродинамических напоров в рассматриваемых сечениях

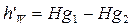. (3.29)

Потеря напора является линейной величиной и измеряется обычно в метрах.