Для элементарной струйки и потока жидкости

Рассмотрим движение жидкости в элементарной струйке между двумя произвольно взятыми сечениями 1-1 и 2-2 (рис. 3.3)

За отрезок времени 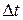в рассматриваемый отсек струйки через сечение 1-1 войдёт некоторое количество

жидкости, равное

Рис. 3.3 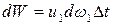. (3.6)

Принятые ранее условия, что движение капельной жидкости происходит без пустот и разрывов сплошной массой, а частицы жидкости не могут переходить из одной струйки в другую позволяют заключить, что за время 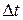через сечение 2-2 должно выйти точно такое же количество жидкости

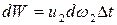. (3.7)

Приравняв правые части уравнений (3.6) и (3.7), получим

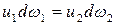. (3.8)

Полученное уравнение (3.8) является уравнением неразрывности для элементарной струйки, т.е. через все сечения элементарной струйки в единицу времени протекает одинаковое количество жидкости, равное расходу элементарной струйки.

Уравнение неразрывности для потока может быть получено в результате интегрирования уравнения неразрывности для элементарной струйки (3.8), после которого запишем:

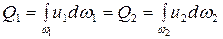. (3.9)

Т.к. правая и левая части уравнения (3.9) согласно зависимости (3.3) выражают расходы в соответствующих сечениях потока, то согласно зависимости (3.4) запишем равенство

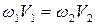, (3.10)

выражающее уравнение неразрывности для потока. Уравнение неразрывности является математической записью закона сохранения массы применительно к движению жидкости постоянной плотности.