На криволинейные поверхности

Первый случай. Цилиндрическая поверхность, давление жидкости с одной стороны – справа (рис 2.25).

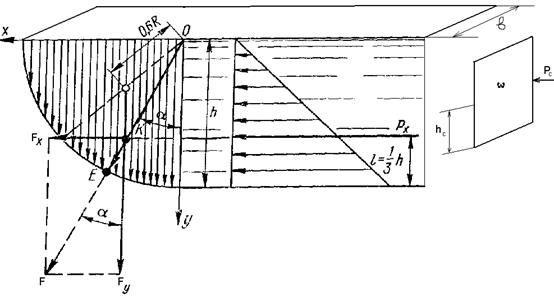
Рис.2.25

1) Выберем оси координат ОУ.

2)Определим горизонтальную (спроектируем) составляющую суммарного гидростатического давления. Она равна произведению силы гидростатического давления на площадь сечения, т.е.

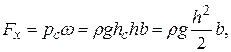
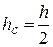, т.к. 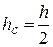. (2.111)

3) Плечо давления горизонтальной составляющей силы

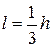, (2.112)

4)Определим вертикальную составляющую суммарного гидростатического давления.

Поскольку силу давления жидкости на стенку можно вычислить так же по объёму эпюры, принимая последнюю за нагрузку, приложенную к стенке, то запишем

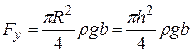. (2.113)

5) Определим равнодействующую

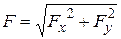. (2.114)

6) Найдём угол наклона линии действия силы F

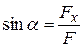. (2.115)

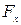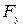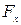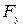7) Графическим способом определим точку приложения силы F. Для этого проводим линию по направлению до пересечения с вертикальной составляющей силой , приложенной в центре тяжести тела давления. От точки пересечения сил и строим параллелограмм и находим равнодействующую силы F. Далее величину F откладываем в масштабе на линии равнодействующей от криволинейной поверхности – точка Е, которая и есть точка приложения равнодействующей силы – центр давления.

Второй случай. Цилиндрическая поверхность, давление жидкости слева. Все расчёты и графическое определение центра давления производятся как и в первом случае (вместо - ).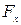

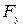Третий и четвёртый случаи построения эпюр гидростатического давления на криволинейные поверхности можно изучить по [ ].

Закон Архимеда

Закон Архимеда о силе, действующей на погруженное в воду тело был сформулирован Архимедом за 250 лет до н.э. В настоящее время он звучит следующим образом: на погруженное в жидкость тело действует выталкивающая сила, равная весу жидкости, вытесненной этим телом.

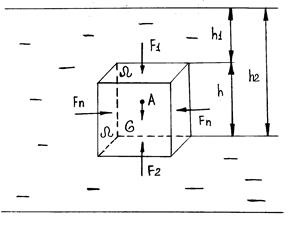
Рис. 2.26

Рассмотрим силы, действующие на погруженное в жидкость тело А (рис. 2.26):

1)боковые силы 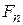. Так как они равны и противоположны, то их равнодействующая равна нулю;

2)сила тяжести тела А, направленная вниз;

3)сила давления жидкости на тело А сверху – ,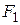

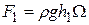; (2.116)

4)сила давления жидкости на тело А снизу – ,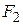

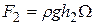; (2.117)

Суммарная сила давления жидкости на погруженное тело, или выталкивающая сила, будет равна

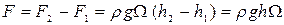. (2.118)

Но т.к. 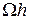– есть объём погруженного тела А, то выталкивающая сила

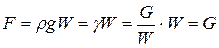. (2.119)

Следовательно, подъёмная, или выталкивающая, сила, действующая на погруженное в жидкость тело, равна весу жидкости, вытесненной данным телом.

Величина выталкивающей силы не зависит от глубины погружения тела и на различной глубине будет постоянной.

Гидродинамика