Давление жидкости на наклонную поверхность

В практике часто встречаются плоские поверхности (щиты, стенки), расположенные под каким-либо углом 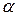к горизонту.

Выведем расчётную зависимость для определения силы давления жидкости на наклонную плоскую стенку (рис.2.18).

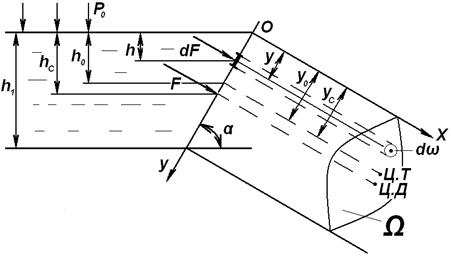
Рис. 2.18

Для этого:

1) выделим элементарную площадку 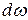, расположенную на глубине h;

2) выберем оси координат, развернём их на прямой угол;

3) обозначим центр тяжести щита (Ц.Т).

На 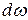будет действовать элементарная сила гидростатического давления

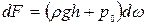, (2.80)

где 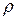– плотность жидкости, кг/м³; 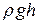– избыточное гидростатическое давление, Па; 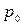– давление на свободной поверхности жидкости, Па.

Суммарная сила гидростатического давления на весь щит равна сумме элементарных сил, действующих по всей смоченной площади щита. Проинтегрируем выражение (2.80) по площади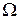

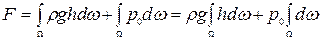. (2.81)

Из рис.2.18 видно, что 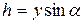, тогда

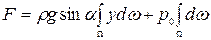, (2.82)

где 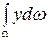– статический момент площади относительно оси ОХ, он равен произведению площади на расстояние от Ц.Т. до оси ОХ, значит

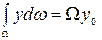_. (2.83)

Из рис.2.18 видно, что 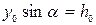. Тогда, с учётом этого, подставив (2.83) в (2.82), получим

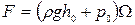. (2.84)

Полная сила давления жидкости на плоскую стенку равна произведению площади стенки на величину гидростатического давления.

Внешняя сила 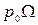приложена в Ц.Т площади, сила избыточного давления приложена ниже Ц.Т, в – Ц.Д (центре давления).

В случае, если 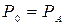(рис. 2.19), на щит будет действовать с одной стороны атмосферное давление, а с другой – давление со стороны жидкости, направленные навстречу друг к другу, то формула (2.84) примет вид

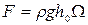. (2.85)

Рис.2.19