Эпюры гидростатического давления на плоские поверхности

Первый случай. Щит вертикальный прямоугольный, жидкость находится с левой стороны (рис. 2.21).

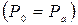Построим эпюру гидростатического давления с указанием ее ординат по всей высоте щита . В любой точке гидростатическое давление

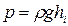, (2.92)

Рис. 2.21

где 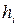- глубина погружения соответствующей точки.

При 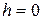избыточное гидростатическое давление 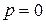. В точке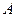 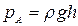; в точке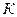 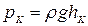. Отложим найденные значения 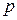в рассматриваемых точках нормально к площадке действия и соединим их вершины линией (прямая 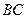). Величина давления зависит от глубины погружения точки и изменяется по закону прямой линии. Эпюра гидростатического давления в рассматриваемом случае будет иметь вид .

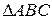Равнодействующая суммарного гидростатического давления жидкости пройдет через центр тяжести 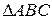на расстоянии 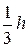от его основания. Точка приложения суммарного избыточного гидростатического давления (точка 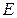) – центр давления.

Суммарная сила гидростатического давления на вертикальный прямоугольный щит равна произведению площади эпюры на ширину щита (например, )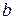

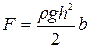. (2.93)

Расстояние от основания эпюры до центра давления называют плечом давления и обозначают через 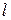. В данном случае

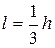. (2.94)

Второй случай. Наклонный прямоугольный щит, давление жидкости с одной стороны (рис. 2.22)

Суммарная сила гидростатического давления 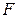определится той же формулой, что и в первом случае.

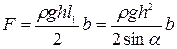, (2.95)

Рис. 2.22

где 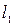- длина щита; .

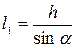Плечо давления в этом случае будет

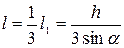. (2.96)

Третий случай. Вертикальный прямоугольный щит, да 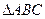вление жидкости с двух сторон (рис. 2.23).

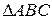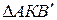Построим эпюры давления справа и слева в виде и . Суммарная сила гидростатического давления слева 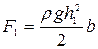, справа .

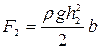Рис. 2.23

Равнодействующая сила гидростатического давления на щит будет равна разности

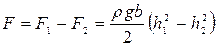. (2.97)

Трапеция 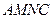представляет эпюру равнодействующей гидростатического давления на щит.

Найдем плечо этой силы, для чего составим уравнение моментов относительно точки .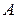

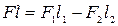, (2.98)

где 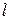, , 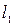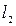- соответствующие плечи давлений суммарных сил , , .

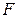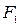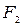Но мы знаем, что

; ,

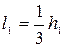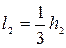поэтому, плечо давления равнодействующей силы 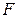на щит может быть определено из следующего выражения

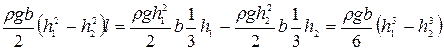, (2.99)

откуда

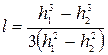. (2.100)

Ординату центра можно определить так же и графическим способом.

Четвертый случай. Наклонный прямоугольный щит, давление жидкости с двух сторон.

Для данного случая суммарное гидростатическое давление определяется аналогичным образом, как и для третьего случая с той лишь разницей, что в указанные формулы вводят синус угла наклона щита ( , , , )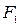

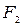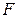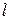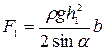и.т.д. (2.101)