Давление жидкости на плоскую горизонтальную поверхность

Рассмотрим сосуд с глубиной воды 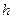. Поскольку давление жидкости в какой- либо точке сосуда зависит от глубины погружения этой точки, то давления в произвольно взятых точках 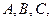будут равны (рис. 2.16):

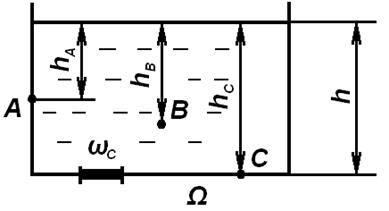
Рис. 2.16

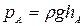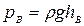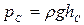; ; . (2.75)

Сила гидростатического давления на горизонтальную площадку 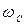будет равна

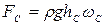_. (2.76)

Сила гидростатического давления на дно сосуда площадью 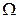определится по формуле

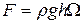. (2.77)

Следовательно, суммарная сила давления жидкости на горизонтальную поверхность равна весу столба жидкости, расположенной над рассматриваемой поверхностью.

Теперь рассмотрим три сосуда различной формы, но с одинаковой площадью дна 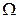. Все сосуды наполнены однородной жидкостью на глубину 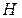(рис. 2.17 а, б, в). На рис. 2.17, б: .

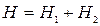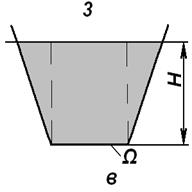
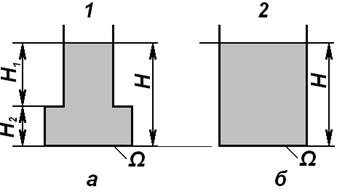
Рис. 2.17

Гидростатическое давление на дно во всех сосудах будет одинаковым и равным

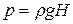. (2.78)

Суммарная сила гидростатического давления так же будет одинаковой и равной

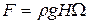. (2.79)

Откуда же в сосуде 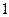берется дополнительная сила по сравнению с сосудом 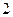и куда пропадает избыток веса жидкости в сосуде 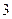по сравнению с сосудом 2? Нет ли здесь противоречия с законами физики?

Законы гидравлики утверждают, что давление жидкости не зависит от формы сосуда, а зависит от глубины погружения площади и её размеров. В этом заключается гидростатический парадокс, который может быть объяснен законом Паскаля.