Синтез регуляторов для контура скорости
В некоторых случаях цифровые автоматизированные электроприводы имеют разомкнутый контур тока, что позволяет обеспечить максимальную частоту пропускания и в контуре скорости при установке цифрового регулятора скорости. Ограничение тока якоря на допустимом уровне при этом достигается использованием нелинейных обратных связей – “отсечек по току” [8]. По этой причине неизменяемая частота системы в контуре тока представляется передаточной функцией ДПФ по управляющему воздействию (напряжению на якоре):
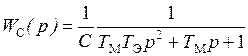 , (5.15)
, (5.15)
где С – коэффициент пропорциональности между скоростью ДПТ и его противо-ЭДС.
Для синтеза регулятора скорости запишем ДЧХ двигателя, силового преобразователя и датчика скорости с учетом того, что ТМ > T0 и ТЭ > T0. ДЧХ (левая) для области низких частот имеет вид:
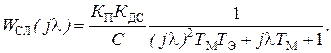 (5.16)
(5.16)
В области высоких частот, учитывая запаздывание, вносимое микро-ЭВМ и равное gТ0, ДЧХ равна:
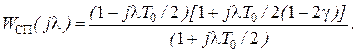
С учетом приведенных выше рекомендаций и необходимости придания контуру скорости астатических свойств по управляющему и возмущающему воздействию примем [6]:
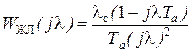 . (5.17)
. (5.17)
Так как разность порядков знаменателя и числителя 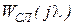 l = 2, находим ДЧХ регулятора скорости из условия:
l = 2, находим ДЧХ регулятора скорости из условия:
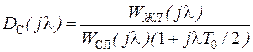 .
.
После подстановки 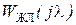 и
и 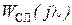 получим ДЧХ регулятора скорости:
получим ДЧХ регулятора скорости:
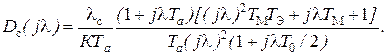 (5.18)
(5.18)
Выполнив необходимые преобразования, получим ДПФ регулятора скорости:
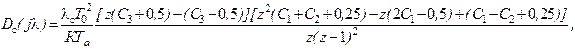
где 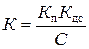 ,
, 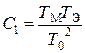 ,
, 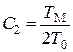 ,
, 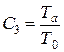 .
.
Для расчета коэффициентов ДПФ регулятора скорости необходимо определить частоту среза lС и 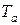 из следующих выражений [6]:
из следующих выражений [6]:
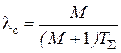 ,
, 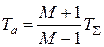 ,
,
где 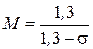 – показатель колебательности, который нужно иметь для получения перерегулирования s, Тå – сумма малых постоянных времени, меньших периода дискретности.
– показатель колебательности, который нужно иметь для получения перерегулирования s, Тå – сумма малых постоянных времени, меньших периода дискретности.
Пример расчета 4. Рассчитаем параметры регулятора скорости, воспользовавшись исходными данными примера расчета 2 и дополнительно приняв коэффициенты передачи датчика скорости КС= 0,1 В×с и противо-ЭДС С = 0,49 В×с. Примем s= 0,05 и найдем показатель колебательности 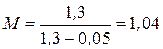 .Сумма малых постоянных времени Тå = 0,5Т0 + gТ0,
.Сумма малых постоянных времени Тå = 0,5Т0 + gТ0, 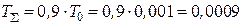 с, находим частоту среза системы и постоянную времени
с, находим частоту среза системы и постоянную времени 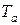 :
:
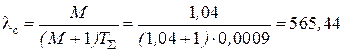 с-1,
с-1,
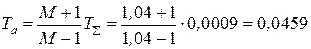 с.
с.
Рассчитаем параметры регулятора скорости, предварительно определив:
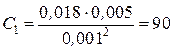 ;
; 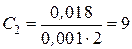 ;
; 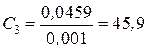 ,
, 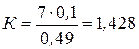 ,
, 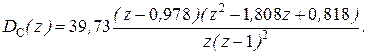
Цифровой регулятор скорости, реализованный на основе полной передаточной функции ДПТ, имеет достаточно сложную структуру, что вызывает увеличение времени на реализацию алгоритма регулятора на микроЭВМ.
В автоматизированных электроприводах с транзисторными силовыми преобразователями прибегают к регулированию тока с помощью время-импульсного релейного регулятора, работающего в скользящем режиме [3]. В этом случае контур тока становится близким к безинерционному звену с коэффициентом передачи 1/КДТ, а передаточная функция непрерывной части системы значительно упрощается до интегрирующего звена:
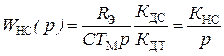 . (5.19)
. (5.19)
Выполним синтез цифрового регулятора скорости для такой структуры электропривода. Для получения ДЧХ неизменяемой части контура скорости выполним над WНС(р) модифицированное z-преобразование с учетом запаздывания в работе микро-ЭВМ, равного gТ0:
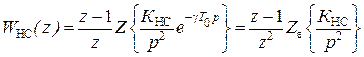 для e = 1 - g,
для e = 1 - g,
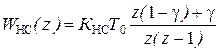 .
.
Затем выполним W-преобразование и за счет подстановки 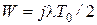 найдем ДЧХ. Опуская промежуточные преобразования, получим:
найдем ДЧХ. Опуская промежуточные преобразования, получим:
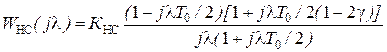 .
.
Примем желаемую ДЧХ разомкнутого контура регулирования скорости с целью придания ему астатических свойств по управлению и возмущению в виде: 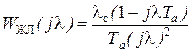 .
.
Учитывая, что в области низких частот 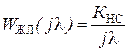 , получим ДЧХ регулятора скорости из условия:
, получим ДЧХ регулятора скорости из условия:
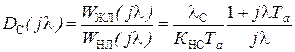 .
.
Выполняя подстановку 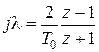 , найдем ДПФ регулятора скорости:
, найдем ДПФ регулятора скорости:
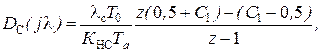 где
где 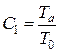 . (5.20)
. (5.20)
Один из способов упрощения динамической структуры систем – “силовой преобразователь – ДПТ” является введение положительной обратной связи по скорости на вход преобразователя, компенсирующей влияние противо-ЭДС ДПТ. В этом случае передаточная функция неизменяемой части системы равна:
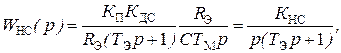 где
где 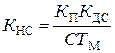
Найдем ДЧХ неизменяемой части системы с учетом времени запаздывания вычислений в микро-ЭВМ, равного gТ0
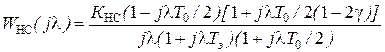 .
.
Примем ДЧХ с учетом необходимого астатизма желаемой системы в виде:
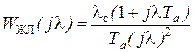 .
.
ДЧХ неизменяемой системы в области низких частот 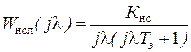 и для нее l= 2 (разность порядков знаменателя и числителя), то ДЧХ регулятора скорости определяется выражением:
и для нее l= 2 (разность порядков знаменателя и числителя), то ДЧХ регулятора скорости определяется выражением:
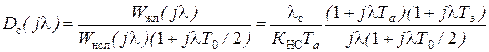 . (5.21)
. (5.21)
Как видно, ДЧХ соответствует ПИД – регулятору. ДПФ регулятора скорости:
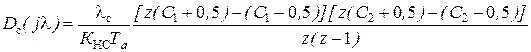 , (5.22)
, (5.22)
где 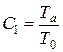 ,
, 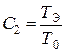 .
.
Пример расчета 5. По исходным данным примера расчета 2 рассчитаем регулятор скорости для электропривода с компенсацией противо–ЭДС двигателя. Так как lС= 565,44 с-1, а Та = 0,0459 с, то получим:
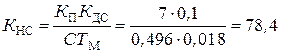 ,
, 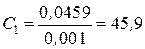 ,
, 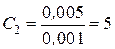 .
.
ДПФ регулятора скорости после соответствующих преобразований равна:
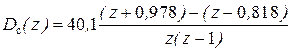 .
.
Дата добавления: 2021-01-11; просмотров: 514;











