Окружающая среда – это все, что находится за пределами системы.
Система характеризуется определенными термодинамическими параметрами (свойствами)(температура, давление, объём, масса, концентрация и др.).
В химической термодинамике используется абсолютная шкала температур, единицей измерения в которой является кельвин (К). Сохранила значение также шкала Цельсия (единица измерения – градус Цельсия, оС). Нуль по шкале Цельсия равен 273,15 К.
В качестве единицы давления в Международной системе (СИ) используют паскаль (Па). Нередко используют также миллиметр ртутного столба (мм рт. ст.) и атмосферу (атм), 1 атм=760 мм рт. ст.=101325 Па =101,325 кПа.
За стандартные условияпринимают температуру 298,15 К (25 оС) и давление 101,325 кПа. Иногда используют нормальные условия(Т=273,15 К, или 0оС, и р=101,325 кПа=1 атм=760 мм рт.ст.).
Термодинамика рассматривает равновесныесостояния системы, т.е. случай, когда термодинамические параметры одинаковы во всех точках системы.
Термодинамика изучает переходы системы из одного состояния в другое. Если переходы происходят при постоянстве некоторых параметров, то они называются:
1) изобарными (р=const);
2) изохорными (V=const);
3) изотермическими (T=const);
4) изобарно-изотермическими(р=const, T=const) и т.д.
Состояние системы описывают термодинамическими функциями состояния системы,или характеристическими функциями. Особенностью термодинамических функций состояния является независимость изменения функции от пути процесса. Их значение определяется только состоянием системы, т.е. параметрами системы (р, Т и др.).
Термодинамические параметры, не зависящие от количества (или массы) вещества, называют интенсивными(р, Т), а зависящие –экстенсивными. Функции состояния являются экстенсивными параметрами, поэтому их относят к 1 моль вещества. Наиболее используемыми являются следующие функции состояния: внутренняя энергия U, энтальпия H, энтропия S и энергия Гиббса G.
Первый закон (начало) термодинамики. Любой процесс подчиняется закону сохранения энергии, выражаемому уравнением
Q = ΔU + W. (3.1)
Уравнение (3.1) означает, что теплота Q, сообщенная системе, расходуется на изменение внутренней энергии системы ΔU и выполнение работы W против внешних сил.
Под внутренней энергией понимают общий запас энергии системы за исключением потенциальной энергии положения системы и кинетической энергии движения системы как целого. Внутренняя энергия представляет собой способность системы к совершению работы или передаче теплоты. Определить абсолютное значение внутренней энергии системы невозможно т.к., с одной стороны, это означало бы возможность состояния системы с энергией равной нулю, а с другой стороны, современной науке известны не все формы энергии. Тем не менее, можно найти изменение внутренней энергии системы при переходе из одного состояния в другое:
ΔU = U2 – U1. (3.2)
Теплота Q представляет собой меру хаотического движения частиц данной системы. Теплота передается от более нагретого тела к менее нагретому телу.
Работа W является мерой энергии, передаваемой от одной системы к другой под действием тех или иных сил.
Теплота и работа не являются функциями состояния, т.е. они зависят от пути процесса.
Единицей измерения теплоты и работы является джо- уль (Дж). Теплота, подводимая к системе, считается положительной (Q>0), а теплота выделяемая системой, – отрицательной (Q<0).
Формула (3.1) является математическим выражением первого закона термодинамики: энергия не возникает и не исчезает, но лишь переходит из одной формы в другую.
Энтальпия. Работа, производимая системой, может быть разделена на работу против внешнего давления рΔV и работу против всех прочих сил W′:
W = W′ + рΔV,
где р – внешнее давление; ΔV – изменение объема ( ΔV=V2 – V1 ; V2 – объем системы в конечном состоянии или объем продуктов реакции; V1 – объем системы в начальном состоянии или объем исходных веществ).
Если из всех внешних сил на систему действует только постоянное давление (р=const; изобарный процесс), то уравнение (3.1) запишется следующим образом:
Qp=ΔU+рΔV=U2–U1+pV2– pV1=(U2 +pV2)– (U1 + pV1). (3.3)
Сумму
U+pV=H (3.4)
называют энтальпией. Энтальпия является термодинамическим свойством, так же как масса, объем и т.д. Одновременно энтальпия – функция состояния системы, т.е. ее изменение не зависит от пути процесса, а определяется только состоянием системы в конце и начале процесса. Энтальпия является экстенсивным свойством, т.е. ее численное значение пропорционально количеству вещества. Единицей измерения энтальпии является джоуль на моль (Дж/моль).
Подставив уравнение (3.3) в (3.4), получим уравнение
Qp=H2–H1=ΔH. (3.5)
Из уравнения (3.5) следует, что энтальпия – это теплота, выделяемая или поглощаемая в ходе изобарного процесса (тепловой эффект изобарного процесса равен изменению энтальпии в ходе этого процесса).
Если понимать под Н2 энтальпии всех конечных продуктов реакции (ΣΗf), а под H1 – энтальпии всех исходных веществ (ΣΗi), то уравнение (3.5) для химической реакции запишется следующим образом:
Qp = ΔrH= ΣΗf - ΣΗi, (3.6)
где ΔrH – изменение энтальпии в ходе химической реакции, или энтальпия реакции.
Для изохорного процесса (V=const, ΔV=0) уравнение (3.2) примет вид
Qv = ΔU = U2 – U1, (3.7)
т.е. тепловой эффект изохорного процесса равен изменению внутренней энергии системы.
Для химической реакции, протекающей при постоянном объёме, уравнение (3.7) по аналогии с (3.6) можно записать так:
Qv = ΔrU= ΣUf - ΣUi . (3.8)
Химические процессы, протекающие с выделением теплоты, называются экзотермическими(ΔU<0; ΔH<0), а с поглощением теплоты – эндотермическими(ΔU>0; ΔH>0).
Химические уравнения, для которых указаны тепловые эффекты, называются термохимическими уравнениями. В термохимических уравнениях обычно указывают также агрегатное состояние веществ, концентрации растворов и другие факторы, влияющие на величину теплового эффекта реакции. Для того чтобы отнести тепловой эффект к 1 моль какого-либо вещества, в термохимических уравнениях иногда используют дробные стехиометрические коэффициенты. Приведем несколько примеров термохимических уравнений:
Н2(г) + 1/2О2(г) = Н2О(ж),  кДж;
кДж;
Н2(г) + 1/2О2(г) = Н2О(г), 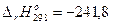 кДж;
кДж;
С(гр) + О2(г) = СО2(г), 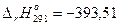 кДж;
кДж;
С(алм) + О2(г) = СО2(г), 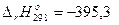 кДж,
кДж,
где г – газ; ж – жидкость; гр – графит; алм – алмаз.
В выражении 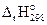 индексы имеют следующее значение: 1) r означает, что изменение энтальпии относится к химической реакции; 2) правый нижний индекс (298) означает температуру системы; 3) правый верхний индекс (о) указывает на стандартное состояние веществ, участвующих в реакции. За стандартное состояние твердых веществ принимают состояние чистого кристаллического вещества, находящегося при стандартных условиях (298 К, 101,325 кПа) в виде стабильной в этих условиях модификации. Стандартное состояние жидких веществ – чистая жидкость, а газообразных – чистый газ при стандартных условиях.
индексы имеют следующее значение: 1) r означает, что изменение энтальпии относится к химической реакции; 2) правый нижний индекс (298) означает температуру системы; 3) правый верхний индекс (о) указывает на стандартное состояние веществ, участвующих в реакции. За стандартное состояние твердых веществ принимают состояние чистого кристаллического вещества, находящегося при стандартных условиях (298 К, 101,325 кПа) в виде стабильной в этих условиях модификации. Стандартное состояние жидких веществ – чистая жидкость, а газообразных – чистый газ при стандартных условиях.
Закон Гесса. Открыт в 1840 г. российским ученым Г.И. Гессом. Тепловой эффект реакции, протекающей при постоянном давлении или постоянном объеме, не зависит от пути протекания реакции и определяется только природой и состоянием исходных веществ и конечных продуктов.
Рассмотрим процесс получения оксида углерода (IV) из графита:
С(гр) + О2(г) = СО2(г) 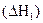 .
.
Эту же реакцию можно осуществить в две стадии через образование оксида углерода (II):
С(гр) + 1/2О2(г) = СО(г) 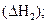
СО(г) + 1/2 О2(г) = СО2(г) 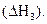
Эти реакции можно представить следующей схемой:

В соответствии с законом Гесса можно записать:
ΔН1 = ΔН2 + ΔН3 или ΔН1 - ΔН2 - ΔН3 = 0. (3.9)
Процессы, в которых система после ряда последовательных превращений возвращается в исходное состояние, называются круговыми процессами или термодинамическими циклами. Метод циклов используется для вычисления различных термодинамических свойств веществ. Так, в рассматриваемом цикле ΔН1 и ΔН3 могут быть относительно легко определены экспериментально, и затем из уравнения (3.9) можно найти величину ΔН2, которую по объективным причинам сложно измерить:
ΔН2 = ΔН1 - ΔН3.
Закон Гесса имеет ряд следствий. Рассмотрим два из них.
Первое следствие закона Гесса. Энтальпия химической реакции равна сумме энтальпий образования продуктов реакции за вычетом суммы энтальпий образования исходных веществ.
Энтальпия образования вещества В ( 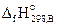 ) – это энтальпия реакции образования 1 моль соединения из простых веществ, устойчивых при стандартных условиях.Например, энтальпия образования нитрата натрия равна энтальпии реакции
) – это энтальпия реакции образования 1 моль соединения из простых веществ, устойчивых при стандартных условиях.Например, энтальпия образования нитрата натрия равна энтальпии реакции
Na(кр) + ½N2(г) + 3/2О2(г) = NaNO3(кр)
и составляет  кДж/моль.
кДж/моль.
Энтальпия образования простых веществ при стандартных условиях принята равной нулю. Стандартные энтальпии образования большого количества химических соединений определены экспериментально и приводятся в справочных изданиях.
Энтальпия химической реакции в общем виде
аА + bB = dD + eE (3.10)
определяется по уравнению
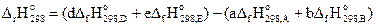 .
.
(3.11)
Пример 3.1.Рассчитать стандартную энтальпию реакции
Al2(SO4)3(т) = Al2O3(т) + 3SO3(г), если стандартные энтальпии образования кристаллических сульфата алюминия и оксида алюминия и газообразного оксида серы (VI) составляют -3441; -1675 и -396 кДж/моль соответственно.
Решение. Из первого следствия закона Гесса
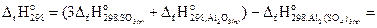 =[3(-396) +(-1675)] – (-3441)= 578 кДж.
=[3(-396) +(-1675)] – (-3441)= 578 кДж.
Пример 3.2. Реакция горения этана выражается термохимическим уравнением
С2Н6(г) + 3,5 О2(г) = 2СО2(г) + 3Н2О(ж) , ΔrНo = -1559, 87 кДж.
Вычислить энтальпию образования этана, если стандартные энтальпии образования СО2(г) и Н2О(ж) составляют -394,38 и -237,19 кДж/моль соответственно.
Решение. На основании первого следствия из закона Гесса можно записать:
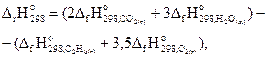
откуда

Пример 3.3.Вычислить количество теплоты, которое выделяется при окислении 20 г сульфида цинка кислородом. 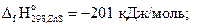
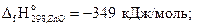

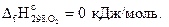
Решение. Из уравнения реакции
2ZnS + 3O2 = 2ZnO + 2SO2
на основании первого следствия из закона Гесса можно записать:
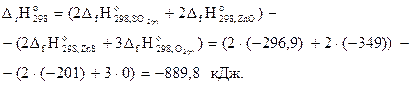
Это количество энергии (889,8 кДж) выделяется при окислении 2 моль сульфида цинка, т.е. 2(65+32)=194 г. Составим пропорцию:
при окислении 194 г ZnS выделяется (-889,8 кДж),
- “ - 20 г ZnS - “ - х кДж),
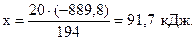
Пример 3.4.Определить 
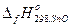 исходя из следующих данных:
исходя из следующих данных:
1) Sn(бел) + О2(газ) = SnO2(кр) – 580,8 кДж;
2) 2SnО(кр) + О2(газ) = 2 SnO2(кр) – 589,6 кДж.
Решение. Из уравнения (1) следует, что тепловой эффект этой реакции равен стандартной энтальпии образования SnO2(кр) 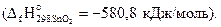
Запишем выражение для теплового эффекта реакции (2), используя первое следствие закона Гесса:
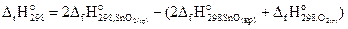 .
.
Отсюда выразим стандартную энтальпию образования SnO(кр):
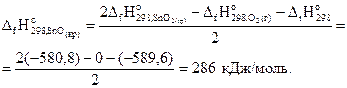
Второе следствие закона Гесса. Энтальпия химической реакции равна сумме энтальпий сгорания исходных веществ за вычетом суммы энтальпий сгорания продуктов реакции.
Энтальпия сгорания вещества В (  ) – это энтальпия реакции окисления кислородом 1 моль соединения до образования высших оксидов.Например, энтальпия реакции сгорания метанола есть изменение энтальпии следующей реакции:
) – это энтальпия реакции окисления кислородом 1 моль соединения до образования высших оксидов.Например, энтальпия реакции сгорания метанола есть изменение энтальпии следующей реакции:
СН3ОН + 3/2О2 = СО2 + 2Н2О.
Стандартные энтальпии сгорания большого количества органических соединений определены экспериментально и приводятся в справочных изданиях.
Энтальпия химической реакции в общем виде (3.10) определяется по уравнению
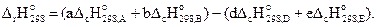
(3.12)
Уравнение (3.12) имеет особое значение для органических веществ.
Пример 3.5.Рассчитать стандартную энтальпию реакции
C2H4(г) + Н2(г) = С2Н6(г) , если стандартные энтальпии сгорания газообразных этана и этилена составляют -1559,88 и -1410,97 кДж/моль соответственно.
Решение. На основании второго следствия закона Гесса запишем:
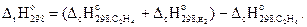
Стандартная энтальпия сгорания водорода равна стандартной энтальпии образования воды, т.е.
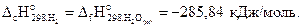
Подставляя численные значения величин в выражение для стандартной энтальпии реакции, получим


Пример 3.6.Рассчитать стандартную энтальпию реакции образования As2O5, используя следующие данные:
1) 4As(кр)+3О2(г)=2As2O3(кр) – 1313,6 кДж;
2) As2O3(кр)+О2(г)= As2O5(кр) – 311,2 кДж.
Решение: Из уравнения (1) в соответствии с определением энтальпии образования вещества следует, что 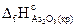 составляет половину теплового эффекта этой реакции, т.е. (-1213,6/2)=-606,8 кДж/моль.
составляет половину теплового эффекта этой реакции, т.е. (-1213,6/2)=-606,8 кДж/моль.
Для уравнения (2) на основании 1-го следствия закона Гесса запишем:

откуда
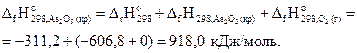
Дата добавления: 2016-10-07; просмотров: 2546;











