Оптимизация передаточного числа редуктора

Одни и те же стационарные режимы работы привода могут быть обеспечены различным образом, так как электродвигатели выпускаются на различную частоту вращения, а редукторы изготавливаются с различными передаточными отношениями. С повышением частоты вращения электродвигателя уменьшаются его габариты и масса, но возрастают габариты и масса редуктора, так что стоимость привода вцелом изменяется незначительно. Но если привод работает в циклическом режиме с частыми пусками и торможениями, то динамические характеристики привода начинают играть ведущую роль, так как влияют на производительность рабочей машины вцелом. В таком случае возникает задача оптимизации передаточного числа редуктора с целью повышения быстродействия привода. При условии что М_С=const и η_Р = 1 уравнение движения исполнительного органа можно записать в виде

М_Р - М_СИО = (J_ВД i_Р² + J_ВИО) ,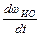

где J_ВД - момент инерции вала двигателя

J_ВД = J_РД + J_М + J_ВШР;

J_РД, J_М , J_ВШР - моменты инерции ротора двигателя, соединительной муфты и ведущей шестерни редуктора соответственно,

J_ВИО - момент инерции вала исполнительного органа

J_ВИО = J_ВШР + J_М + J_ИО,

J_ВШР, J_М , J_ИО - моменты инерции ведомой шестерни редуктора, соединительной муфты ведомого вала редуктора и исполнительного органа соответственно;

ω_ИО, М_СИО - частота вращения и момент сопротивления исполнительного органа.

Это выражение относительно ускорения исполнительного органа запишется

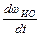= ε_ИО = .

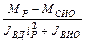Для определения передаточного числа редуктора, соответствующего максимальному ускорению привода возьмем производную по передаточному отношению редуктора от ускорения и приравняем её нулю. После преобразований получаем

i_{Р ОПТ} = + .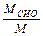

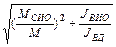Максимальное ускорение и замедление исполнительного органа можно достичь в том случае, когда М_СИО = 0.

В этом случае

i_{Р ОПТ} = .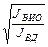

Практически наиболее выгодное передаточное отношение редуктора определяют по минимуму произведения приведенного момента инерции привода на квадрат передаточного отношения редуктора.