Многомассовые механические системы.

Механическая часть электропривода может содержать элементы конечной жесткости. Наиболее часто такими элементами являются канаты, валопроводы, соединяющие двигатель с редуктором муфты, содержащие пружинные или резиновые элементы. При наличии таких элементов приведение к валу двигателя, рассмотренное ранее для одномассовой системы выполнять нельзя. При рассмотрении движения таких систем вводится понятие коэффициента жесткости (С) упругого элемента. Он представляет собой коэффициент пропорциональности между линейной ΔL или угловой Δφ деформациями и возникающими в упругом элементе силой F_У или моментом М_У

F_У = С₁ ΔL;

М_У = С₂ Δφ.

Коэффициенты жесткости С₁ и С₂ определяются геометрическими размерами упругого элемента и зависят от материала из которого он изготовлен. Для упругого стержня при его растяжении или сжатии коэффициент жесткости [Н/м] определяется как

С₁ = SE/L,

где L - длина стержня, м;

S - площадь поперечного сечения стержня, м²;

Е - модуль упругости, Па.

Для вала радиусом R при его кручении коэффициент жесткости

С₂ = J_SG/L,

где J_S = πR⁴/2 - момент инерции поперечного сечения вала, м⁴;

G - модуль упругости кручения, Па;

L - длина вала, м.

Чем больше коэффициент жесткости упругого элемента, тем меньшая деформация в нем возникает. Величина обратная коэффициенту жесткости называется податливостью.

Приведение коэффициента жесткости упругого элемента к валу двигателя выполняют по следующим формулам:

для упругого вала при кручении

С = С₂/i²;

для упругого поступательно движущегося элемента при растяжении и сжатии

С = С₁ρ²,

где ρ - радиус приведения кинематической схемы между валом двигателя и упругим элементом.

При параллельном соединении упругих элементов эквивалентная жесткость определяется

С_ЭКВ = С₁ + С₂ + С₃ +...+ С_N,

а при последовательном

= + + +...+ .

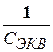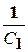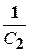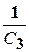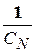Если учитывается только один упругий элемент, то расчетная механическая система называется двухмассовой.