Краткая запись теорем 4 – 6.

4.f(x) = g(x) ⇔ h(x)f(x) = h(x)g(x), где h(x) ≠0 и h(x) имеет смысл в ОДЗ данного уравнения.

5.f(x) = g(x) ⇔ (f(x))ⁿ=(g(x))ⁿ , где f(x) ≥ 0, g(x) ≥ 0 и n=2k (чётное число).

6.log_a f(x) = log_a g(x) ⇔ f(x) = g(х), где f(х) > 0, g(х) > 0 и а > 0 и a≠1

3) Преобразование данного уравнения в уравнение – следствие. Проверка корней

Если в процессе решения уравнения применяем теоремы 4-6, не проверив выполнения ограничительных условий, то получим уравнение-следствие.

Например.

а)х – 1 = 3; х = 4

Умножим обе части на (х – 2):

(х – 2)(х – 1) = 3(х – 2); х = 4 и х = 2 – посторонний корень⇒ проверка!

б)ln(2x–4) =ln(3x–5)

Потенцируем 2х – 4 = 3х – 5; х = 1, но при этом значении уравнение не имеет смысла ⇒ искать ОДЗ или проверка.

Примеры

№1. Решить уравнение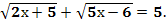

Решение.

Первый этап — технический.

На этом этапе, как мы отмечали выше, осуществляют преобразования заданного уравнения по схеме (1) => (2) => (3) => (4) => ... и находят корни последнего (самого простого) уравнения указанной цепочки.

Последовательно получаем:

;

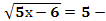
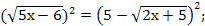
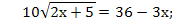
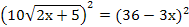
100(2х+5)² = 1296 – 216х + 9х²;

9х² – 416х + 796 = 0;

х₁ = 2, х_{2 =}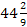

Второй этап — анализ решения.

На этом этапе, анализируя проведенные преобразования, отвечают на вопрос, все ли они были равносильными.

Третий этап — проверка.

Подставим поочередно каждое из найденных значений переменной в исходное уравнение.

х₂ = 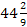- посторонний корень.

Ответ:х = 2.

№2. Решить уравнение ln (х + 4) + ln (2х + 3) = ln (1 - 2х).

Решение.

Первый этап.

Воспользуемся правилом «сумма логарифмов равна логарифму произведения». Оно позволяет заменить выражение ln (х + 4) + ln (2х + 3)выражением ln (х + 4)(2х + 3).

Тогда заданное уравнение можно переписать в виде:

ln (х + 4)(2х + 3) = ln (1 - 2х).

Потенцируя, получаем:

(х + 4)(2х + 3) = (1 - 2х); 2х² + 8х + Зх + 12 = 1 - 2х; 2х² + 13х + 11 = 0; х₁ = -1, х₂ = -5,5.

Второй этап.

В процессе решения произошло расширение ОДЗ уравнения, значит, обязательна проверка.

Третий этап.

Поскольку, кроме расширения ОДЗ уравнения, никаких других неравносильных преобразований в процессе ре­шения уравнения не было, проверку можно выполнить по ОДЗ исходного уравнения. Она задается системой неравенств

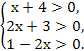
Значение х = -1удовлетворяет этой системе неравенств, а значение х = -5,5не удовлетворяет уже первому неравенству, это посторонний корень.

Ответ: -1.

4) О потере корней.

Укажем две причины потери корней при решении уравнений:

1. Деление обеих частей уравнения на одно и то же выражение h(х)(кроме тех случаев, когда точно известно, что всюду в области определения уравнения выполняется условие h(х) ≠0);

2. Сужение ОДЗ в процессе решения уравнения.

С первой причиной бороться нетрудно: приучайте себя переходить от уравнения

f(х)h(х) = g{х)h{х)к уравнению h(x)(f(x) – g(x))=0 (а не к уравнению f(x)=g(x)).Может быть, даже есть смысл вообще запретить себе деление обеих частей уравнения на одно и то же выражение, содержащее переменную.