Теоремы равносильности уравнений.

Определения равносильных уравнений и уравнений - следствий

Определение 1. Два уравнения с одной переменной f(х) = g(х) и р(х) = h(х) называют равносильными, если множества их корней совпадают.

Иными словами, два уравнения называют равносильными, если они имеют одинаковые корни или если оба уравнения не имеют корней.

Например,

уравнения х² - 4 = 0 и (х + 2)(2^x - 4) = 0 равносильны, оба они имеют по два корня: 2 и -2. Равносильны и уравнения х²+1=0 и 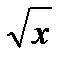= -3, поскольку оба они не имеют корней.

Определение 2. Если каждый корень уравнения f(x) = g(х) ₍₁₎

является в то же время корнем уравнения р(х) = h(х), (2)

То уравнение (2) называют следствием уравнения (1).

Например, уравнение х - 2 = 3 имеет корень х = 5,

а уравнение (х - 2)² = 9 имеет два корня: х₁ = 5, х₂ = -1.

Корень уравнения х - 2 = 3 является одним из корней уравнения (х - 2)² = 9.

Значит, уравнение (х - 2)² = 9 — следствие уравнения х - 2 = 3.

Очевидным является следующее утверждение.

Два уравнения равносильны тогда и только тогда, когда каждое из них является следствием другого.

Решение уравнения осуществляется в три этапа.

Первый этап — технический. На этом этапе осуществляют преобразования по схеме

(1) → (2) → (3)→ (4) → ... и находят корни последнего (самого простого) уравнения указанной цепочки.

Второй этап — анализ решения. На этом этапе, анализируя проведенные преобразования, отвечают на вопрос, все ли они были равносильными.

Третий этап — проверка. Если анализ, проведенный на втором этапе, показывает, что некоторые преобразования могли привести к уравнению-следствию, то обязательна проверка всех найденных корней их подстановкой в исходное уравнение.

Реализация этого плана связана с поисками ответов на четыре вопроса.

Как узнать, является ли переход от одного уравнения к другому равносильным преобразованием?

Какие преобразования могут перевести данное уравнение в уравнение-следствие?

Если мы в конечном итоге решили уравнение-следствие, то как сделать проверку в случае, когда она сопряжена со значительными вычислительными трудностями?

В каких случаях при переходе от одного уравнения к другому может произойти потеря корней и как этого не допустить?

Теоремы равносильности уравнений.

«Спокойные теоремы» гарантируют равносильность преобразований без каких-либо дополнительных условий, их использование не причиняет решающему никаких неприятностей.

«Беспокойные теоремы» работают лишь при определенных условиях, а значит, могут доставить некоторые неприятности при решении уравнений.

«Спокойные теоремы»:

Теорема 1. Если какой-либо член уравнения перенести из одной части уравнения в другую с противоположным знаком, то получится уравнение, равносильное данному.

Теорема2. Если обе части уравнения возвести в одну и ту же нечетную степень, то получится уравнение, равносильное данному.

Теорема3. Показательное уравнение а^f(x) = а^g(x), (где а > 0, a≠1) равносильно уравнению

f(x) = g(х).

Прежде чем формулировать теоремы 4—6, напомним еще об одном понятии, связанном с уравнениями.

Определение 3. Областью определения уравнения f(х) = g(х)или областью допустимых значений переменной (ОДЗ) называют множество тех значений переменной х,при которых одновременно имеют смысл выражения f(х)и g(х).

«Беспокойные теоремы»:

Теорема 4.Если обе части уравнения f(x) = g(х) умножить на одно и то же выражение h(х), которое:

а) имеет смысл всюду в области определения (в области допустимых значений) уравнения

f(x) = g(х);

б) нигде в этой области не обращается в 0,

то получится уравнение f(x)h(x) = g(x)h(x), равносильное данному в его ОДЗ.

Следствием теоремы 4 является еще одно «спокойное» утверждение:если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному.

Теорема 5.Если обе части уравнения f(x) = g(х) неотрицательны в ОДЗ уравнения, то после возведения обеих его частей в одну и ту же четную степень n получится уравнение (f(x))ⁿ=(g(x))ⁿ равносильное данному в его ОДЗ.

Теорема 6.Пусть а > 0 и a ≠ 1, x — решение системы неравенств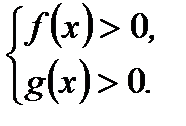

Тогда логарифмическое уравнение log_a f(x) = log_a g(x) равносильно на множестве X

уравнению f(x) = g(х)