Со второй причиной бороться сложнее.
Рассмотрим, например, уравнение lg х2 = 4 и решим его двумя способами.
Первый способ. Воспользовавшись определением логарифма, находим:
х2= 104; х₁ =100, х2 =-100.
Второй способ. Имеем: 2lgх =4; lg x= 2; х =100.
Обратите внимание: при втором способе произошла потеря корня — «потерялся» корень х =-100. Причина в том, что вместо правильной формулы lg х2 =2lg|x| мы воспользовались неправильной формулой lg х2 = 2lg х, сужающей область определения выражения, из нее «выпал» открытый луч (-∞; 0), где как раз и находится «потерявшийся» при втором способе решения корень уравнения.
Вывод: применяя при решении уравнения какую-либо формулу (особенно тригонометрическую), следите за тем, чтобы области допустимых значений переменной для правой и левой части формулы были одинаковыми.
Работа в классе.
Задание 1. Верно ли, что уравнение 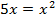 является следствием уравнения
является следствием уравнения 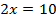 на множестве действительных чисел. Ответ: да.
на множестве действительных чисел. Ответ: да.
Задание 2.Равносильно ли уравнение 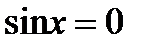 уравнению:
уравнению:
а) 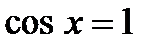 ; б)
; б) 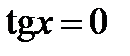 ; в)
; в)  ; г)
; г) 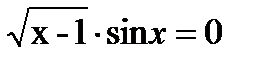 ?
?
Задание 3.Решите уравнения: а) 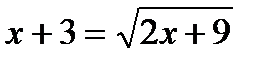 ; б)
; б) 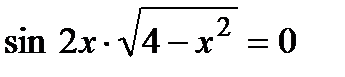 ;
;
Домашняя работа.
№ 1. Равносильно ли уравнение 2x = 256
уравнению:
а) log2 x =3; б) х2 – 9х + 8 = 0; в) 3 х2 – 24х = 0.
№ 2. Равносильны ли уравнения:
а) 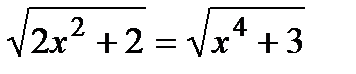 и
и 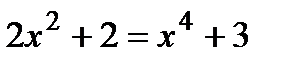 ?
?
б) 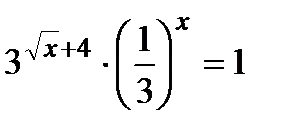 и
и 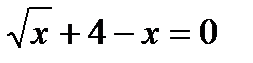 ?
?
№3. Решите уравнения:
а) 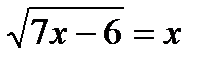 ; б)
; б) 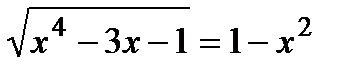 .
.
Дата добавления: 2021-01-11; просмотров: 472;











