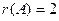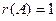Геометрический смысл систем линейных уравнений.

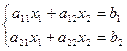
Каждое из уравнений задаёт некоторую прямую в плоскости.

Система несовместна:	Система совместна:
прямые параллельны	определённая неопределённая, прямые пересекаются прямые совпадают

Система из 2 уравнений на 3 неизвестных: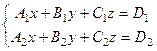

Каждое уравнение задаёт плоскость в пространстве.

Определённой система быть не может, так как 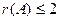, тогда .

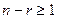Система несовместна:	Система совместная, неопределённая:
плоскости параллельны	плоскости пересекаются по прямой плоскости совпадают

Две плоскости пересекаются по прямой, а что есть пересечение двух 3-мерных пространств в 4-мерном? Плоскость или прямая? Представить наглядно мы это себе не можем, однако тут на помощь геометрии приходит абстрактная алгебра: системы линейных уравнений. С их помощью ответить на данный вопрос очень легко. Если уравнения двух пространств:

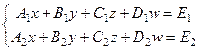
то очевидно, что ранг основной и расширенной матриц либо 1, либо 2.

Если ранг основной и расширенной матриц равен 2, то 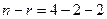свободных переменных. Тогда пересечение 2-мерно.

Если ранг основной и расширенной матриц равен 1, то тогда есть 3 свободных переменных, то есть эти пространства совпадают.

Если ранг основной матрицы 1, а расширенной 2, то решений нет, и они параллельны, (нет ни одной общей точки).

Таким образом, два 3-мерных пространства не могут пересекаться по прямой или в точке, так же, как две плоскости не могут пересекаться в точке. Пространства пересекаются по плоскости.

3 трёхмерных пространства пересекаются по прямой: основная матрица 3*4, одна свободная переменная.

Лекция 10. 12.12.2020.