Проектирование ригеля

Расчет неразрезного ригеля. Ригель многопролетного перекрытия представляет собой элемент рамной конст­рукции. При свободном опирании концов ригеля на на­ружные стены и равных пролетах ригель можно рассчи­тывать как неразрезную балку. При этом возможен учет образования пластических шарниров, приводящих к пе­рераспределению и выравниванию изгибающих момен­тов между отдельными сечениями.

Сущность расчета статически неопределимых желе­зобетонных конструкций с учетом, перераспределения усилий. При некотором значении нагрузки напряжения в растянутой арматуре из мягкой стали достигают преде­ла текучести. С развитием в арматуре пластических де­формаций (текучести) в железобетонной конструкции возникает участок больших местных деформаций, назы­ваемый пластическим шарниром.

В статически определимой конструкции, например в свободно лежащей балке (рис. XI. 11,а), с появлением пластического шарнира под влиянием взаимного поворо­та частей балки и развивающегося значительного проги­ба высота сжатой зоны сокращается, в результате чего достигается напряжение в сжатой зоне

σ_b =R_b наступа­ет разрушение.

Иначе ведет себя статически неопределимая конст­рукция (рис. XI.11,6). Здесь с появлением пластического шарнира повороту частей балки, развитию прогиба сис­темы и увеличению напряжений в сжатой зоне препятст­вуют лишние связи (защемления на опорах); возникает стадия II а, при которой σ_s=σ_y, но σ_b<R_b

Поэтому при дальнейшем увеличении нагрузки разрушение в пласти­ческом шарнире не произойдет до тех пор, пока не поя­вятся новые пластические шарниры и не выключатся лишние связи.

В статически неопределимой системе возникновение пластического шарнира равносильно выключению лишней связи и снижению на одну степень статической неопределимости системы. Для рассмотренной балки с двумя защемленными концами возникновение первого пластического шарнира превращает ее в систему, один раз статически неопределимую; потеря геометриче­ской неизменяемости может наступить лишь с образова­нием трех пластических шарниров — на обеих опорах и в пролете.

В общем случае потеря геометрической неизменяемо­сти системы с п лишними связями наступает с образова­нием n+1 пластических шарниров.

В статически неопределимой конструкции после по­явления пластического шарнира при дальнейшем увели­чении нагрузки происходит перераспределение изгибаю­щих моментов между отдельными сечениями. При этом деформации в пластическом шарнире нарастают, но зна­чение изгибающего момента остается прежним: М =R_s A_s z_b

Плечо внутренней пары сил z_b после образования пластического шарнира при дальнейшем росте нагрузки увеличивается незначительно и практически принимается постоянным (рис. XI.11,в).

Рассмотрим на примере балки, защемленной на двух опорах, последовательность перераспределения изгибаю­щих моментов. С появлением пластического шарнира на одной из опор при нагрузке F₀ (рис. XI. 12, а) балка при­обретает новую схему — с одной защемленной и второй шарнирной опорами (рис. XI.12, б). При дальнейшем по­вышении нагрузки балка работает по этой новой схеме. С момента появления пластического шарнира на дру­гой опоре при увеличении нагрузки на ∆₁ F₀ балка пре­вращается в свободно опертую (рис. XI.12,б). Образо­вание пластического шарнира в пролете при дополни­тельной нагрузке ∆₂ F₀ превращает балку в изменяемую систему, т. е. приводит к разрушению.

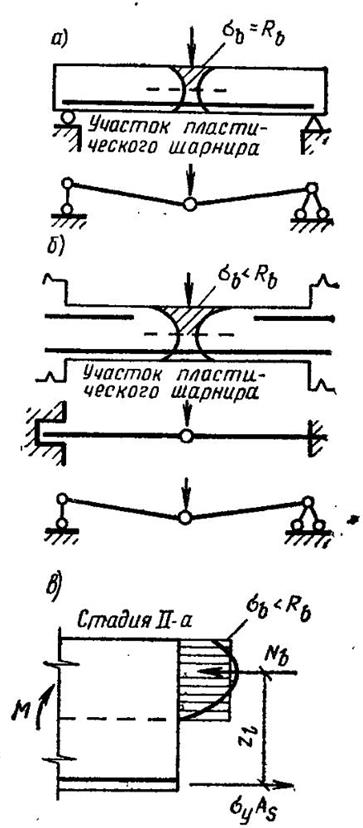
Рис. Xl.ll. Схема образования пластического шарнира в желе­зобетонных балках

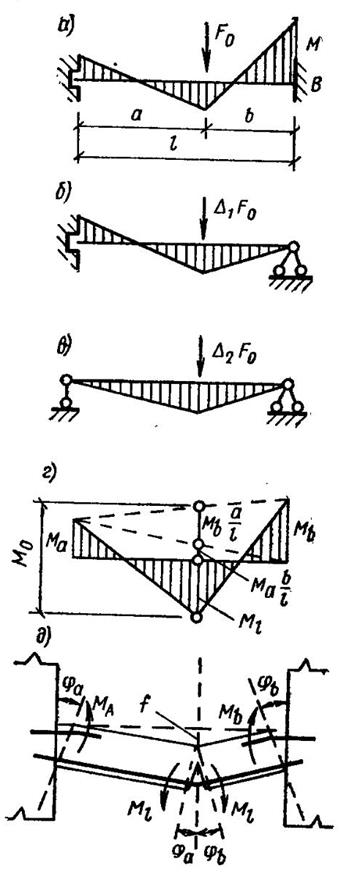
Рис. XI.12. Эпюры перераспре­деления изгибающих моментов в статически неопределимой балке

.

Предельные расчетные моменты в расчетных сечени­ях (в пластических шарнирах) равны: М_a — на опоре А; М_b — на опоре; M_l— в пролете (рис.XI.12, г).

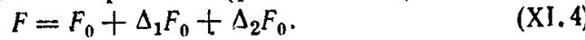
В предельном равновесии—непосредственно перед раз­рушением — изгибающие моменты балки можно найти статическим или кинетическим способом.

Статический способ. Запишем значение пролетного момента:

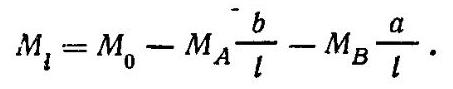
Отсюда уравнение равновесия

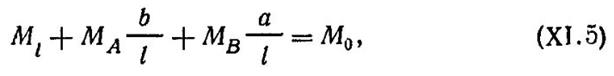
где M₀=Fab/l — момент статически определимой свободно лежащей балки.

Из уравнения (XI.5) следует, что сумма пролетного момента в сечении и долей опорных моментов, соответст­вующих этому сечению, равна моменту простой балки М₀. Кроме того, из уравнения (XI.5) вытекает, что несущая способность статически неопределимой конструкции не зависит от соотношения значений опорных и пролетного моментов и не зависит от последовательности образова­ния пластических шарниров. Последовательность эта мо­жет быть назначена произвольно, необходимо лишь соб­людать уравнение равновесия. Однако изменение соот­ношения моментов в сечениях меняет значение нагрузки, вызывающей образование первого и последнего пласти­ческих шарниров, а также меняет ширину раскрытия трещин в первом пластическом шарнире.

Кинематический способ. Балка в предельном равнове­сии рассматривается как система жестких звеньев, сое­диненных друг с другом в местах излома пластическими шарнирами (рис. XI. 12, д). Если прогиб балки под си­лой F равен f, то углы поворота звеньев

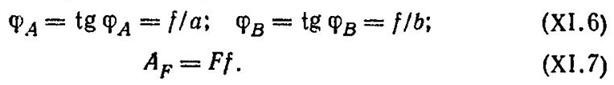Виртуальная работа внутренних усилий — изгибающих моментов в пластических шарнирах

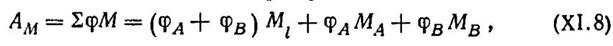а с учетом полученных выше значений

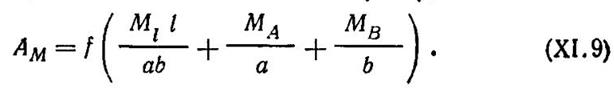
Уравнение виртуальных работ

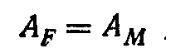
или

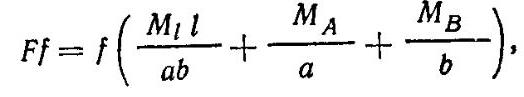
откуда расчетная предельная сила

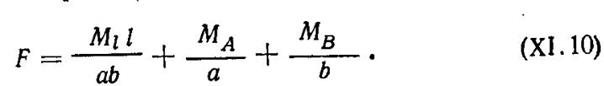
Если умножить левую и правую части уравнения (XI.10) на ab/l, то получим найденное выше статическим спосо­бом уравнение равновесия (XI.5).

Расчет и конструирование статически неопределимых железобетонных конструкций по выравненным моментам позволяет облегчить армирование сечений, что особенно важно для монтажных стыков на опорах сборных кон­струкций; позволяет стандартизировать и осуществить в необходимых случаях одинаковое армирование сварными сетками и каркасами там, где при расчете по упругой схеме возникают различные по значению изгибающие мо­менты. При временных нагрузках расчет по выравнен­ным моментам по сравнению с расчетом по упругой схе­ме может давать 20—30 % экономии стали в арматуре.

Величина перераспределенного момента не оговари­вается, но должен производится расчет по предельным состояниям второй группы. Практически ограничение раскрытия трещин в первых пластических шарнирах до­стигается ограничением выравненного момента с тем, чтобы он не слишком резко отличался от момента в уп­ругой схеме и приблизительно составлял не менее 70 %.

Чтобы обеспечить условия, отвечающие предпосылке метода предельного равновесия, т. е. возможность обра­зования пластических шарниров и развития достаточных местных деформаций при достижении конструкцией пре­дельного равновесия, следует соблюдать конструктив­ные требования:

1)конструкция должна быть запроектирована так, чтобы причиной ее разрушения не могли быть срез сжа­той зоны или раздавливания бетона от главных сжимаю­щих напряжений;

2)армирование сечений, в которых намечено образо­вание пластических шарниров, следует ограничивать так, чтобы относительная высота сжатой зоны ξ≤0,35;

3)следует применять арматурные стали с площадкой

текучести или сварные сетки из обыкновенной арматур­ной проволоки.

На действие динамических нагрузок (сейсмика, удар­ная взрывная волна и т. п.) железобетонные статически неопределимые конструкции также целесообразно рас­считывать с учетом образования пластических шарниров.

Если конструкция заармирована стержневой армату­рой без площадки текучести, то после достижения каким-либо моментом условного предельного значения М_0,2 при условном пределе текучести σ_0,2 рост момента не приоста­навливается, а замедляется. Несущая способность кон­струкции в этом случае определяется предельным удли­нением арматуры или предельной прочностью бетона сжатой зоны.

Перераспределение усилий в статически неопредели­мой железобетонной конструкции происходит и на более ранней стадии работы под нагрузкой — под влиянием из­менения жесткости опорных и пролетных сечений вслед­ствие образования и раскрытия трещин в растянутых зо­нах элементов. Хотя такого рода перераспределение уси­лий не оказывает заметного влияния на перераспределе­ние усилий в предельном равновесии — перед образова­нием пластических шарниров, однако оно существенно влияет на работу конструкции в эксплуатационной ста­дии и поэтому учитывается в расчетах.

Для неразрезных балок упрощенный способ учета та­кого рода перераспределения усилий состоит в следую­щем. Опорные моменты вычисляют как в упругой системе и умножают на поправочные коэффициенты, оцениваю­щие неодинаковую жесткость опорных и пролетных сече­ний. Далее по исправленным опорным моментам обыч­ным путем вычисляют пролетные моменты. Значения по­правочных коэффициентов к опорным моментам при рас­пределенной нагрузке или нескольких сосредоточенных грузах:

для средних опор многопролетных балок

для средней опоры двухпролетной балки

для первой промежуточной опоры многопролетных ба­лок— по среднему значению коэффициента λ из приве­денных двух формул.

В этих формулах β=B₁/ B_sup— отношение жесткости сечений с трещинами в пролете и на опоре.

Более подробные данные приведены в «Инструкции по расчету статически неопределимых железобетонных кон­струкций с учетом перераспределения усилий» (Стройиздат, 1975).

Расчет неразрезного ригеля как упругой системы слу­жит основой для следующего перераспределения изгиба­ющих моментов. Расчетный пролет ригеля принимают равным расстоянию между осями колонн; в первом про­лете при опирании на стену расчетный пролет считается от оси опоры на стене до оси колонны. Нагрузка на ри­гель от панелей может быть равномерно распределенной (при пустотных или сплошных панелях) или сосредото­ченной (при ребристых панелях). Если число сосредото­ченных сил, действующих в пролете ригеля, более четы­рех, то их приводят к эквивалентной равномерно распре­деленной нагрузке. Для предварительного определения собственного веса ригеля размеры его сечения прини­мают

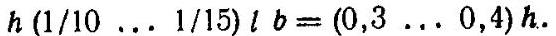
Изгибающие моменты и поперечные силы неразрез­ной балки при равных или отличающихся не более чем на 20 % пролетах определяют по таблицам (приложе­ние X):

для равномерно распределенной нагрузки

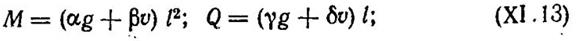для сосредоточенных нагрузок

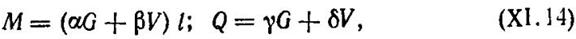где α ,β — табличные коэффициенты при определении М от соответ­ствующих загружений постоянной и временной нагрузкой; γ,δ — таб­личные коэффициенты при определении Q от соответствующих за­гружений постоянной и временной нагрузкой.

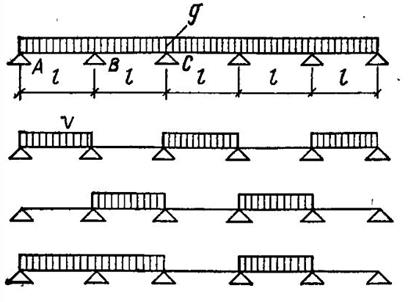
При расположении временной нагрузки через один пролет получают максимальные моменты в загружаемых пролетах; при расположении временной нагрузки в двух смежных пролетах и далее через один пролет получают максимальные по абсолютному значению моменты на опоре (рис. XI.13). В неразрезном ригеле целесообразно ослабить армирование опорных сечений и упростить мон­тажные стыки. Поэтому с целью перераспределения мо­ментов в ригеле к эпюре моментов от постоянных нагрузок и отдельных схем невыгодно расположенных времен­ных нагрузок прибавляют добавочные треугольные эпю­ры с произвольными по знаку и значению надопорными ординатами (рис. XI.14). При этом ординаты выравнен­ной эпюры моментов в расчетных сечениях должны сос­тавлять не менее 70 %, вычисленных по упругой схеме. На основе отдельных загружений строят огибающие эпюры М и Q. Возможен также упрощенный способ рас­чета неразрезного ригеля по выравненным моментам, состоящий в том, что в качестве расчетной выравненной эпюры моментов принимают эпюру моментов упругой неразрезной балки, полученную для максимальных про­летных моментов (при расположении временной нагруз­ки через один пролет). Расчетным па опоре будет сечение ригеля по грани колонны. В этом сечении изгибающий момент

Момент M₁ имеет большее (по абсолютной величине) значение со стороны пролета, загруженного только посто­янной нагрузкой; поэтому в формулу (XI. 13) следует подставлять значение поперечной силы Q, соответствую­щее загружению этого пролета. По моменту M₁ уточня­ют размер поперечного сечения ригеля и по значению ξ≈0,35 принимают

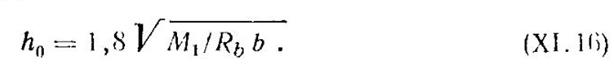
Сечение продольной арматуры ригеля подбирают по М в четырех нормальных сечениях: в первом и среднем пролетах, па первой промежуточной опоре и на средней опоре. Расчет поперечной арматуры по Q ведут для трех наклонных сечений: у первой промежуточной опоры сле­ва и справа и у крайней опоры.